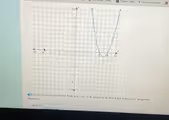
The Correct Answer and Explanation is:
Based on the graph provided in the image, the correct equation for the parabola is y = (1/4)(x – 1)² – 4.
Explanation:
The image displays a graph of a parabola on a coordinate plane. To find the equation that represents this curve, we first identify its key characteristics from the graph. The vertex, which is the minimum point of this upward opening parabola, is clearly located at the coordinates (1, -4). The points where the parabola intersects the x axis, known as the x intercepts, are at (–3, 0) and (5, 0).
Using the vertex, we can employ the vertex form of a quadratic equation, which is y = a(x – h)² + k. In this formula, (h, k) are the coordinates of the vertex. By substituting the observed vertex (1, –4) into the equation, we get a partial equation: y = a(x – 1)² – 4.
The next step is to determine the value of ‘a’, the coefficient that dictates the parabola’s vertical stretch or compression and its direction of opening. We can solve for ‘a’ by substituting the coordinates of any other point on the curve into our equation. Using the x intercept (5, 0) is a convenient choice. We replace y with 0 and x with 5:
0 = a(5 – 1)² – 4
0 = a(4)² – 4
0 = 16a – 4
Solving this simple linear equation for ‘a’ gives us the following:
4 = 16a
a = 4/16, which simplifies to a = 1/4.
The positive value of ‘a’ confirms the parabola opens upwards, as shown in the graph. By inserting this value of ‘a’ back into our equation, we arrive at the final vertex form: y = (1/4)(x – 1)² – 4.
This equation accurately defines the parabola shown. We can verify this using the other x intercept (–3, 0). If we substitute x = –3, the equation should yield y = 0.
y = (1/4)(–3 – 1)² – 4
y = (1/4)(–4)² – 4
y = (1/4)(16) – 4
y = 4 – 4 = 0.
This confirmation reinforces that the equation is correct.
