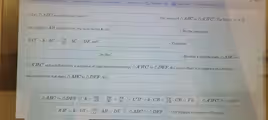
The Correct Answer and Explanation is:
Based on the text visible in the images, here is the correct answer and a detailed explanation.
The Correct Answer
CPCTC is an abbreviation for Corresponding Parts of Congruent Triangles are Congruent.
In the context of the statement “∠A ≅ ∠D because…”, the reason is that they are corresponding parts of congruent triangles. This reasoning is the definition of CPCTC itself, which is used after triangle congruence (for example, △ABC ≅ △DEF) has been established.
Explanation
CPCTC, or Corresponding Parts of Congruent Triangles are Congruent, is a fundamental theorem in geometry. This principle states that if two triangles are proven to be congruent, then every corresponding part of one triangle is also congruent to its counterpart in the other triangle. This includes all three corresponding angles and all three corresponding sides.
Before you can use CPCTC, you must first establish that the two triangles are indeed congruent. Geometers use several accepted postulates and theorems for this purpose. The most common methods are Side-Side-Side (SSS), where all three sides of one triangle are congruent to the three corresponding sides of another. Another is Side-Angle-Side (SAS), which requires two sides and the included angle to be congruent. There is also Angle-Side-Angle (ASA), which uses two angles and the included side, and Angle-Angle-Side (AAS), which involves two angles and a non-included side.
Once you have successfully used one of these methods to prove, for example, that triangle ABC is congruent to triangle DEF (written as △ABC ≅ △DEF), you can then apply CPCTC. This theorem serves as the justification for making further conclusions. For instance, if you proved the triangles were congruent using SSS, you can then use CPCTC to state that ∠A ≅ ∠D, ∠B ≅ ∠E, and ∠C ≅ ∠F.
It is important to distinguish congruence from similarity, another concept visible in the image. Congruent triangles are identical in size and shape. Similar triangles (like △ABC ~ △GEC mentioned in the image) have the same shape but may have different sizes. Their corresponding angles are congruent, but their corresponding sides are proportional, not necessarily equal. CPCTC specifically applies only to congruent figures, providing a powerful tool for solving complex geometric proofs.
