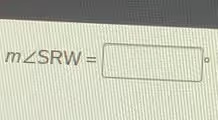
The Correct Answer and Explanation is:
The correct answer for the measure of angle SRW cannot be provided because the image is incomplete. The question “m∠SRW = [ ]°” is presented without any accompanying geometric figure, diagram, or additional information. In geometry, finding the measure of a specific angle requires context about its relationship to other geometric elements.
To solve for the measure of angle SRW, one would typically use a given diagram and apply established geometric principles. For instance, the Angle Addition Postulate might be relevant. This would apply if angle SRW is composed of two smaller adjacent angles, say angle SRT and angle TRW. In that case, the measure of angle SRW would be the sum of the measures of the two smaller angles. Another possibility involves linear pairs. If a point, let’s call it P, lies on the same line as S and R, then angle SRW and angle PRW might form a linear pair, meaning their measures sum to 180 degrees. Knowing one would allow you to find the other.
The angle could also be a part of a polygon. If SRW is a vertex of a triangle, its measure depends on the other two angles, as all three must sum to 180 degrees. If the triangle is isosceles with base SW, then angle RSW would be equal to angle RWS, which could help. If angle SRW is an interior angle of a quadrilateral, its value would depend on the other three angles and the properties of that specific shape, such as a parallelogram, rectangle, or rhombus where angle properties are well defined. If the points S, R, and W lie on a circle, the angle’s measure would relate to the arc it intercepts. For example, if R is the center, angle SRW is a central angle equal to its intercepted arc. If R is on the circle, it is an inscribed angle, which is half its intercepted arc.
Without the visual diagram or the given conditions, any numerical answer would be a guess. Please provide the full problem for a precise calculation.
