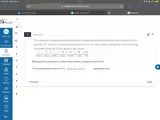
The Correct Answer and Explanation is:
Based on the provided data, the correct answer is 0.35.
Explanation
The problem asks for the sample proportion of customer arrivals that are “at or greater than 4”. A sample proportion is a statistic that represents the fraction of observations in a sample that possess a specific characteristic. To find it, you must divide the number of observations with the desired characteristic by the total number of observations in the sample.
First, we need to determine the total number of observations. The data is presented in two rows, each containing ten numbers. This means the total sample size is 20, as there are 20 one-minute intervals recorded.
Next, we identify the specific characteristic of interest, which is the number of customer arrivals being “at or greater than 4”. This requires us to count every instance in the data set where the number is 4 or 5. We must carefully examine all 20 data points:
5, 2, 4, 0, 4, 3, 2, 4, 3, 2
2, 3, 3, 2, 4, 2, 2, 4, 5, 2
By reviewing the data, we can count the occurrences that meet our condition.
In the first row, the numbers 5, 4, 4, and 4 satisfy the condition. This gives us four instances.
In the second row, the numbers 4, 4, and 5 satisfy the condition. This gives us three instances.
Combining these, the total number of intervals with four or more customer arrivals is 4 plus 3, which equals 7.
Finally, we calculate the sample proportion by dividing the count of these specific instances (7) by the total sample size (20). The calculation is 7 ÷ 20, which equals 0.35. The question asks for the result to be rounded to two decimal places. Since our result is already 0.35, no further rounding is necessary. Therefore, the sample proportion is 0.35, meaning that in 35% of the observed intervals, four or more customers arrived.
