The correct answer and explanation is:
The correct perimeter of the polygon LMNPQ is 12 + 4√2 units, which is approximately 17.66 units.
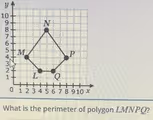
To find the perimeter of the polygon, we must calculate the length of each of its five sides and then add these lengths together. The polygon is on a coordinate plane, so we can determine the coordinates of each vertex first: L is at (4, 2), M is at (2, 4), N is at (5, 8), P is at (8, 4), and Q is at (6, 2).
We use the distance formula, d = √((x₂ – x₁)² + (y₂ – y₁)²), to find the length of each segment.
- Length of QL: This is a horizontal segment. We can find its length by subtracting the x-coordinates: |6 – 4| = 2 units.
- Length of LM: Using the coordinates for L(4, 2) and M(2, 4):
d = √((2 – 4)² + (4 – 2)²) = √((-2)² + 2²) = √(4 + 4) = √8 units. - Length of MN: Using the coordinates for M(2, 4) and N(5, 8):
d = √((5 – 2)² + (8 – 4)²) = √(3² + 4²) = √(9 + 16) = √25 = 5 units. - Length of NP: Using the coordinates for N(5, 8) and P(8, 4):
d = √((8 – 5)² + (4 – 8)²) = √(3² + (-4)²) = √(9 + 16) = √25 = 5 units. - Length of PQ: Using the coordinates for P(8, 4) and Q(6, 2):
d = √((6 – 8)² + (2 – 4)²) = √((-2)² + (-2)²) = √(4 + 4) = √8 units.
Finally, we sum the lengths of all the sides to get the total perimeter:
Perimeter = QL + LM + MN + NP + PQ
Perimeter = 2 + √8 + 5 + 5 + √8
Perimeter = 12 + 2√8
To simplify, we can write √8 as √(4 * 2), which is 2√2.
Perimeter = 12 + 2(2√2) = 12 + 4√2 units.
Using a calculator, √2 is approximately 1.414, so the perimeter is about 12 + 4(1.414) = 12 + 5.656 = 17.656, which rounds to 17.66 units.
