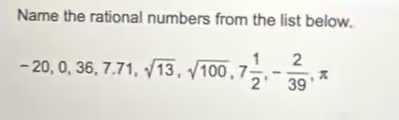
The Correct Answer and Explanation is:
The rational numbers from the list are: -20, 0, 36, 7.71, √100, 7 1/2, and -2/39.
A rational number is a number that can be expressed as a fraction or quotient, p/q, where p and q are both integers and the denominator, q, is not zero. To determine which numbers from the list fit this definition, we can examine each one individually.
First, we consider the integers in the list: -20, 0, and 36. All integers are rational because they can be written as a fraction with a denominator of 1. For example, -20 can be written as -20/1, 0 can be written as 0/1, and 36 can be written as 36/1. Since they all fit the p/q format, they are rational.
Next, we look at the decimal 7.71. This is a terminating decimal, meaning it has a finite number of digits after the decimal point. All terminating decimals are rational because they can be converted into a fraction with a power of ten in the denominator. The number 7.71 is equivalent to the fraction 771/100, which is a ratio of two integers. Therefore, 7.71 is a rational number.
The number √100 is the square root of 100. Since 100 is a perfect square (10 × 10 = 100), the square root of 100 simplifies to the integer 10. As we have already established, all integers are rational, so √100 is a rational number.
The mixed number 7 1/2 can be converted into an improper fraction. By multiplying the whole number by the denominator and adding the numerator, we get (7 × 2) + 1 = 15. The improper fraction is 15/2. This is a ratio of two integers, so 7 1/2 is rational.
The number -2/39 is already presented in the form of a fraction with an integer numerator (-2) and a non-zero integer denominator (39), directly fitting the definition of a rational number.
The remaining numbers, √13 and π, are irrational. The number 13 is not a perfect square, so its square root results in a non-terminating, non-repeating decimal, which cannot be written as a simple fraction. Pi (π) is a famous transcendental number whose decimal representation also continues forever without repeating. Thus, these two numbers are not rational.
