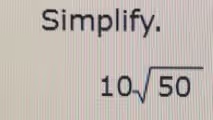
The Correct Answer and Explanation is:
The correct answer is 50√2.
Here is a detailed explanation of the simplification process.
To simplify the expression 10√50, our goal is to make the number inside the square root, known as the radicand, as small as possible. We achieve this by finding and extracting any perfect square factors from the radicand. A perfect square is a number that is the product of an integer with itself, such as 4 (2×2), 9 (3×3), or 25 (5×5).
The first step is to focus on the radical part of the expression, which is √50. We need to find the largest perfect square that divides evenly into 50. Let’s consider the factors of 50. The pairs of factors are (1, 50), (2, 25), and (5, 10). Looking at these factors, we can see that 25 is a perfect square. This is the key to simplifying the radical.
We can rewrite 50 as the product of 25 and 2. So, the expression √50 becomes √(25 × 2).
Next, we use the product property of square roots, which states that the square root of a product is equal to the product of the square roots of its factors. In mathematical terms, this is √(a × b) = √a × √b. Applying this property, we can split √(25 × 2) into √25 × √2.
We know that the square root of 25 is 5. Therefore, √25 × √2 simplifies to 5 × √2, or 5√2. This means that √50 is equivalent to 5√2.
Now, we substitute this simplified radical back into the original expression. The original expression was 10√50. Replacing √50 with 5√2 gives us 10 × (5√2).
The final step is to multiply the numbers outside the radical, which are 10 and 5. Multiplying these coefficients gives us 10 × 5 = 50. The √2 part remains unchanged.
Combining these results, the expression 10√50 simplifies completely to 50√2. The expression is fully simplified because the number remaining inside the radical, 2, has no perfect square factors other than 1.
