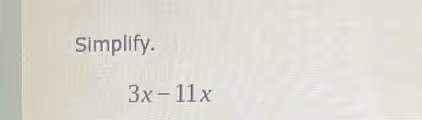
The Correct Answer and Explanation is:
Correct Answer: -8x
The problem requires the simplification of the algebraic expression 3x – 11x. In algebra, simplifying an expression means rewriting it in its most compact and straightforward form. This often involves combining terms that are similar.
The key concept to apply here is the combining of “like terms.” Like terms are terms within an expression that have the same variable or variables raised to the same power. In the expression 3x – 11x, both terms, 3x and 11x, are considered like terms because they both contain the same variable, x, raised to the same power (which is 1).
To combine like terms, you perform the arithmetic operation (in this case, subtraction) on their coefficients. The coefficient is the number that is multiplied by the variable. For the term 3x, the coefficient is 3. For the term 11x, the coefficient is 11.
The operation is to subtract the second coefficient from the first one:
3 – 11 = -8
Once you have the new coefficient, you keep the common variable part, which is x. By attaching the variable x to the new coefficient -8, we get the simplified term.
Therefore, the expression 3x – 11x simplifies to -8x.
Think of it like having objects. If you have 3 of something (let’s say, 3 “x’s”) and you take away 11 of that same thing, you end up with a deficit of 8 of them, which is represented as -8 “x’s”. The expression is now a single term, -8x, and cannot be simplified any further.
