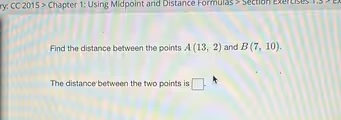
The Correct Answer and Explanation is:
The correct answer is 10.
To find the distance between two points, A(13, 2) and B(7, 10), in a two-dimensional plane, we use the distance formula. This formula is derived from the Pythagorean theorem and is expressed as:
d = √[(x₂ – x₁)² + (y₂ – y₁)²]
Here, (x₁, y₁) represents the coordinates of the first point, A, and (x₂, y₂) represents the coordinates of the second point, B. The ‘d’ stands for the distance between them.
First, we identify the coordinates from the given points:
For point A(13, 2): x₁ = 13 and y₁ = 2.
For point B(7, 10): x₂ = 7 and y₂ = 10.
Next, we substitute these values into the distance formula:
d = √[(7 – 13)² + (10 – 2)²]
Now, we perform the calculations inside the parentheses:
The difference in the x-coordinates is 7 – 13 = -6.
The difference in the y-coordinates is 10 – 2 = 8.
Substituting these results back into the formula gives us:
d = √[(-6)² + (8)²]
Next, we square each of these values. Remember that squaring a negative number results in a positive number:
(-6)² = 36
(8)² = 64
Now the equation looks like this:
d = √[36 + 64]
We then add the two numbers inside the square root symbol:
36 + 64 = 100
Finally, we find the square root of the sum:
d = √100
d = 10
Therefore, the distance between point A(13, 2) and point B(7, 10) is 10 units.
