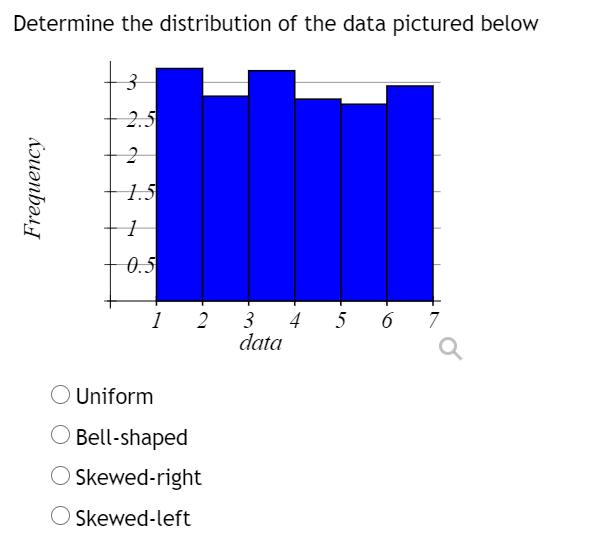
Determine the distribution of the data pictured below Uniform Bell-shaped Skewed-right Skewed-left
Determine the distribution of the data pictured below
Uniform
Bell-shaped
Skewed-right
Skewed-left
The correct answer and explanation is:
The correct answer depends on the shape of the data pictured, which isn’t provided here. However, I’ll explain each distribution type and how to identify them. If you have a specific description or can upload the data or image, feel free to share for precise analysis.
1. Uniform Distribution
- Definition: A uniform distribution has data values evenly spread across the range. Each value has approximately the same frequency.
- Visual Appearance: The histogram or plot appears as a flat, horizontal line or bar heights that are roughly equal.
- Real-Life Example: Rolling a fair die, where each number from 1 to 6 has an equal probability of occurrence.
2. Bell-Shaped Distribution
- Definition: Also called a normal distribution, this shape is symmetric, with most data points clustering around the mean, and frequencies taper off as you move away from the center.
- Visual Appearance: A smooth, bell-like curve. The mean, median, and mode are equal and located at the peak.
- Real-Life Example: Heights of adults or test scores often follow a normal distribution.
3. Skewed-Right Distribution
- Definition: This distribution has a tail that extends to the right. Most data points are concentrated on the left side, with fewer large values stretching to the right.
- Visual Appearance: The histogram has a peak on the left and a gradual slope on the right.
- Real-Life Example: Income distribution, where most people earn less and fewer earn significantly more.
4. Skewed-Left Distribution
- Definition: This distribution has a tail extending to the left. Most data points are concentrated on the right side, with fewer smaller values stretching to the left.
- Visual Appearance: The histogram has a peak on the right and a gradual slope on the left.
- Real-Life Example: Lifespan of certain machines or products, where most last longer and fewer fail early.
To identify the distribution, examine the histogram or plot and compare it to these descriptions. If you share the image or describe it, I can refine the answer.