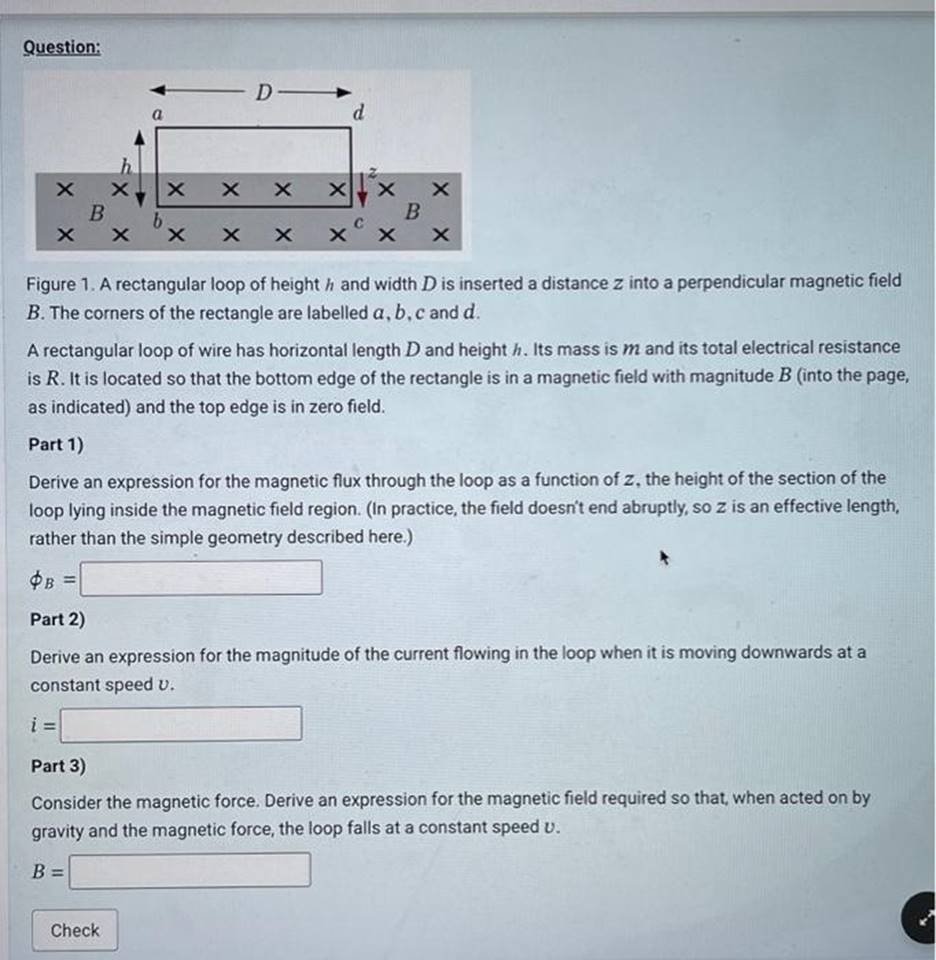
A rectangular loop of height h and width D is inserted a distance z into a perpendicular magnetic field B. The corners of the rectangle are labelled a,b,c and d. A rectangular loop of wire has horizontal length D and height h. Its mass is m and its total electrical resistance is R. It is located so that the bottom edge of the rectangle is in a magnetic field with magnitude B (into the page, as indicated) and the top edge is in zero field. Part 1) Derive an expression for the magnetic flux through the loop as a function of z, the height of the section of the loop lying inside the magnetic field region. (In practice, the field doesn’t end abruptly, so z is an effective length, rather than the simple geometry described here.) ?
B
= Part 2) Derive an expression for the magnitude of the current flowing in the loop when it is moving downwards at a constant speed v. i= Part 3) Consider the magnetic force. Derive an expression for the magnetic field required so that, when acted on by gravity and the magnetic force, the loop falls at a constant speed v. B=
The Correct Answer and Explanation is :
Part 1: Expression for the Magnetic Flux through the Loop
The magnetic flux (\Phi_B) through the rectangular loop is given by:
[
\Phi_B = B \cdot A
]
where (B) is the magnetic field and (A) is the area of the region of the loop inside the magnetic field.
Given that the height of the loop in the magnetic field is (z) and its width is (D), the area (A) of the loop inside the magnetic field is:
[
A = D \cdot z
]
Thus, the magnetic flux through the loop becomes:
[
\Phi_B(z) = B \cdot D \cdot z
]
Part 2: Expression for the Magnitude of the Current Flowing in the Loop
To determine the current flowing in the loop, we apply Faraday’s Law of Induction, which states that the induced emf ((\mathcal{E})) in a loop is the negative rate of change of the magnetic flux through the loop:
[
\mathcal{E} = – \frac{d\Phi_B}{dt}
]
Since (\Phi_B(z) = B \cdot D \cdot z), and (B) is constant while (z) changes as the loop moves with velocity (v), the time derivative of the flux is:
[
\frac{d\Phi_B}{dt} = B \cdot D \cdot \frac{dz}{dt} = B \cdot D \cdot v
]
Thus, the induced emf is:
[
\mathcal{E} = – B \cdot D \cdot v
]
Now, using Ohm’s Law ((V = IR)) for the induced emf, the current (i) in the loop is:
[
i = \frac{\mathcal{E}}{R} = \frac{- B \cdot D \cdot v}{R}
]
The negative sign indicates the direction of the current, but we can ignore it when considering the magnitude:
[
i = \frac{B \cdot D \cdot v}{R}
]
Part 3: Expression for the Magnetic Field Required for Constant Speed
To make the loop fall at a constant speed (v), the net force on the loop must be zero. The forces acting on the loop are:
- Gravitational Force: (F_g = m \cdot g)
- Magnetic Force: The magnetic force on a current-carrying conductor is given by:
[
F_B = i \cdot L \cdot B
]
where (L = D) is the length of the loop in the magnetic field, and (i) is the current we derived earlier. Substituting the expression for (i):
[
F_B = \frac{B \cdot D \cdot v}{R} \cdot D \cdot B = \frac{B^2 \cdot D^2 \cdot v}{R}
]
For the loop to fall at constant speed, the magnetic force (F_B) must balance the gravitational force (F_g):
[
F_B = F_g
]
[
\frac{B^2 \cdot D^2 \cdot v}{R} = m \cdot g
]
Solving for (B), the required magnetic field is:
[
B = \sqrt{\frac{m \cdot g \cdot R}{D^2 \cdot v}}
]
Explanation (300 words)
In this problem, the rectangular loop moves vertically through a magnetic field that varies across its height. The magnetic flux through the loop is determined by the product of the magnetic field (B), the width of the loop (D), and the effective height (z) of the loop inside the field. This gives the magnetic flux (\Phi_B = B \cdot D \cdot z).
When the loop moves downward with a constant velocity (v), Faraday’s Law of Induction comes into play, generating an induced emf. The induced emf is proportional to the rate of change of the magnetic flux, which, in this case, is related to the velocity (v) and the magnetic field (B). Using this induced emf, we calculate the current (i) flowing through the loop as:
[
i = \frac{B \cdot D \cdot v}{R}
]
where (R) is the resistance of the loop.
To maintain a constant speed, the loop must experience zero net force. This requires balancing the gravitational force acting on the loop with the magnetic force, which depends on the current flowing through the loop and the magnetic field. By equating the magnetic force with the gravitational force, we derive the magnetic field (B) required for the loop to fall at a constant speed (v). The required field is:
[
B = \sqrt{\frac{m \cdot g \cdot R}{D^2 \cdot v}}
]
This result shows that the magnetic field required for constant speed is influenced by the loop’s mass, resistance, and dimensions, as well as the velocity of descent.