Which of the following rational functions is graphed below?
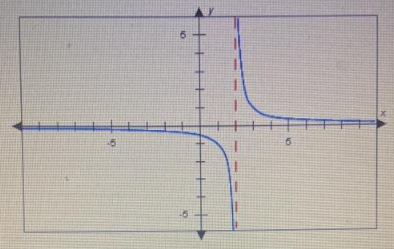
A. F(x) = 1/(x + 2)
B. F(x) = 1/(x – 2)
C. F(x) = 1/2x
D. F(x) = 2/X
The correct answer and explanation is:
To determine which rational function matches the graph, let’s analyze its key features:
Key Features to Identify:
- Vertical Asymptote:
- Occurs where the denominator equals zero (function is undefined).
- Horizontal Asymptote:
- Found by considering the behavior of the function as xx approaches infinity or negative infinity.
- Symmetry:
- Check if the function is symmetric about the origin (odd function) or symmetric about the y-axis (even function).
- Behavior near the Asymptotes:
- Observe how the function approaches the asymptotes (increases or decreases).
Evaluate Each Option:
- F(x)=1x+2F(x) = \frac{1}{x+2}:
- Vertical asymptote at x=−2x = -2, horizontal asymptote at y=0y = 0.
- F(x)=1x−2F(x) = \frac{1}{x-2}:
- Vertical asymptote at x=2x = 2, horizontal asymptote at y=0y = 0.
- F(x)=12xF(x) = \frac{1}{2x}:
- Vertical asymptote at x=0x = 0, horizontal asymptote at y=0y = 0.
- F(x)=2xF(x) = \frac{2}{x}:
- Vertical asymptote at x=0x = 0, horizontal asymptote at y=0y = 0.
Steps:
- Identify the location of the vertical asymptote from the graph.
- Determine how the graph behaves near the asymptotes and at large positive/negative xx.
If you can describe the graph’s asymptotes and behavior (e.g., the vertical asymptote is at x=2x=2, and it approaches zero at large xx), I can match it to one of the functions!