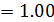
inches.
- Given the following equivalency 2.5 centimeters inches.
a) Identify the two conversion factors.
b) How many centimeters are there in 5.0 inches?
c) How many inches are there in 21.0 centimeters? - A rectangle has a horizontal side measuring and a vertical side measuring 72 . Determine the perimeter. (Horizontal Side + Vertical Side)
- A right triangle has a base of and a height measuring . Determine the area.
- A box has a horizontal side measuring , a vertical side measuring , and a height of . Determine the volume.
- A cylinder has a radius measuring . Determine the area.
- A cylinder has a radius measuring and a height of . Determine the volume.
The correct answer and explanation is:
Let’s address the problems one by one with appropriate explanations and calculations.
1. Given the following equivalency: 2.5 centimeters = 1 inch.
a) Identify the two conversion factors:
- The first conversion factor is:
1 inch=2.5 cm1 \text{ inch} = 2.5 \text{ cm}. - The second conversion factor is:
1 cm=12.5 inch=0.4 inch1 \text{ cm} = \frac{1}{2.5} \text{ inch} = 0.4 \text{ inch}.
b) How many centimeters are there in 5.0 inches?
To convert inches to centimeters, use the conversion factor 1 inch=2.5 cm1 \text{ inch} = 2.5 \text{ cm}: Centimeters=5.0 inches×2.5 cm/inch=12.5 cm\text{Centimeters} = 5.0 \, \text{inches} \times 2.5 \, \text{cm/inch} = 12.5 \, \text{cm}
c) How many inches are there in 21.0 centimeters?
To convert centimeters to inches, use the conversion factor 1 cm=0.4 inch1 \text{ cm} = 0.4 \text{ inch}: Inches=21.0 cm×0.4 inch/cm=8.4 inches\text{Inches} = 21.0 \, \text{cm} \times 0.4 \, \text{inch/cm} = 8.4 \, \text{inches}
2. A rectangle has a horizontal side measuring xx and a vertical side measuring 72. Determine the perimeter.
The perimeter of a rectangle is given by: Perimeter=2×(Length+Width)\text{Perimeter} = 2 \times (\text{Length} + \text{Width})
Here, Length is xx and Width is 72. So, the perimeter is: Perimeter=2×(x+72)\text{Perimeter} = 2 \times (x + 72)
Since xx is not given, the perimeter is expressed in terms of xx.
3. A right triangle has a base of bb and a height of hh. Determine the area.
The area of a right triangle is given by: Area=12×Base×Height\text{Area} = \frac{1}{2} \times \text{Base} \times \text{Height}
Substituting in the given base bb and height hh: Area=12×b×h\text{Area} = \frac{1}{2} \times b \times h
Since bb and hh are not provided, the area is expressed in terms of these variables.
4. A box has a horizontal side measuring xx, a vertical side measuring yy, and a height of zz. Determine the volume.
The volume of a box (rectangular prism) is given by: Volume=Length×Width×Height\text{Volume} = \text{Length} \times \text{Width} \times \text{Height}
Substituting in the given dimensions: Volume=x×y×z\text{Volume} = x \times y \times z
Since the dimensions are represented by variables, the volume is expressed in terms of xx, yy, and zz.
5. A cylinder has a radius of rr. Determine the area.
The surface area of a cylinder is given by the formula: Surface Area=2πr2+2πrh\text{Surface Area} = 2 \pi r^2 + 2 \pi r h
However, to calculate the area, we need to know the height hh. Without that information, the area cannot be determined.
6. A cylinder has a radius of rr and a height of hh. Determine the volume.
The volume of a cylinder is given by the formula: Volume=πr2h\text{Volume} = \pi r^2 h
Substituting in the given radius rr and height hh: Volume=πr2h\text{Volume} = \pi r^2 h
This is the general formula for the volume of a cylinder. Again, without specific values for rr and hh, the answer is expressed in terms of these variables.
Summary of Calculations:
- Conversion factors: 1 inch=2.5 cm1 \text{ inch} = 2.5 \text{ cm} and 1 cm=0.4 inch1 \text{ cm} = 0.4 \text{ inch}.
- Perimeter of a rectangle: 2×(x+72)2 \times (x + 72) (in terms of xx).
- Area of a right triangle: 12×b×h\frac{1}{2} \times b \times h.
- Volume of a box: x×y×zx \times y \times z.
- Volume of a cylinder: πr2h\pi r^2 h (requires height).
Each of these formulas requires specific measurements to provide numerical answers, but they are presented here in their general forms.