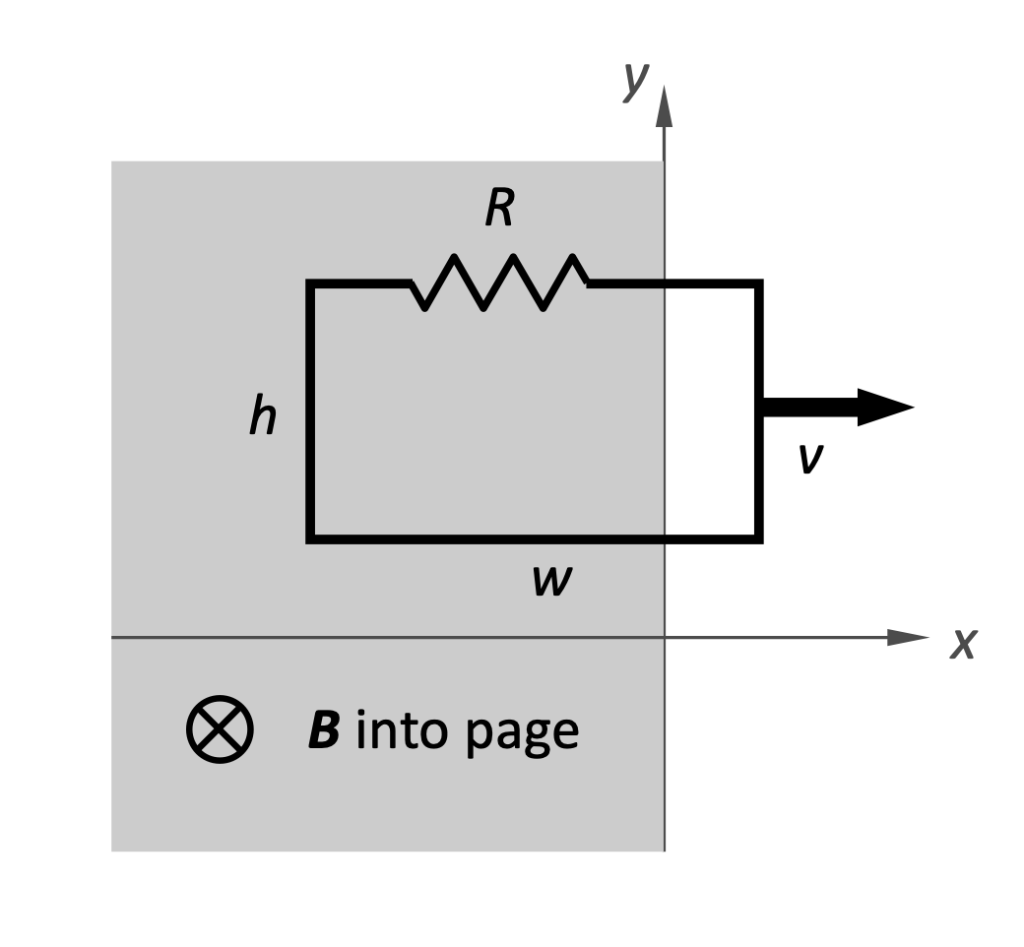
A rectangular wire loop of height h, width w, and net electrical resistance R lies in the x-y plane. As shown in the figure below, the entire region x < 0=”” of=”” space=”” is=”” occupied=”” by=”” a=”” constant,=”” uniform=”” magnetic=”” field=”” which=”” points=”” in=”” the=”” ã¢â‚¬â€œz=”” direction=”” (into=”” the=”” page).=”” in=”” order=”” to=”” determine=”” the=”” magnitude=”” of=”” this=”” field,=”” a=”” student=”” pulls=”” the=”” wire=”” loop=”” out=”” of=”” the=”” magnetic=”” field=”” region=”” at=”” a=”” constant=”” velocity=”” v=”” in=”” the=”” +x-direction,=”” and=”” measures=”” the=”” current=”” i=”” induced=”” in=”” the=”” loop=”” during=”” this=””>
I = 17 μA
R = 35 ohms
h = 3 cmÂÂ
w = 8 cm
v = 2 cm/sec
a) What is the direction of the current induced in the wire loop?
b)What is the magnitude B of the magnetic field?
ÂÂ
The Correct Answer and Explanation is :
a) Direction of the Induced Current:
When the rectangular wire loop is pulled out of the magnetic field region, the magnetic flux through the loop decreases. According to Lenz’s Law, the induced current will flow in a direction that opposes this decrease in flux. To oppose the reduction in magnetic flux, the induced current must generate a magnetic field that points into the page (in the -z direction). Using the right-hand rule, if the fingers of your right hand curl in the direction of the current, your thumb points in the direction of the magnetic field created by that current. For the magnetic field to point into the page, the current must flow in a counterclockwise direction when viewed from above. Therefore, the induced current flows counterclockwise in the loop.
b) Magnitude of the Magnetic Field (B):
The induced electromotive force (EMF) in the loop is given by Faraday’s Law:
[ \mathcal{E} = -\frac{d\Phi_B}{dt} ]
where ( \Phi_B ) is the magnetic flux through the loop. The magnetic flux is the product of the magnetic field strength ( B ), the area ( A ) of the loop, and the cosine of the angle between the magnetic field and the normal to the loop’s surface. Since the magnetic field is uniform and points into the page (perpendicular to the loop), the angle is 0 degrees, and ( \cos(0^\circ) = 1 ). Thus, the magnetic flux is:
[ \Phi_B = B \times A ]
The area ( A ) of the rectangular loop is:
[ A = h \times w = 0.03\,\text{m} \times 0.08\,\text{m} = 0.0024\,\text{m}^2 ]
The change in magnetic flux ( d\Phi_B ) is the product of the magnetic field strength ( B ), the area ( A ), and the change in time ( dt ). The change in time is the time it takes for the loop to move out of the magnetic field region. The velocity ( v ) of the loop is 0.02 m/s, and the width ( w ) of the loop is 0.08 m. Therefore, the time ( dt ) is:
[ dt = \frac{w}{v} = \frac{0.08\,\text{m}}{0.02\,\text{m/s}} = 4\,\text{s} ]
The induced EMF ( \mathcal{E} ) is also related to the induced current ( I ) and the resistance ( R ) of the loop:
[ \mathcal{E} = I \times R ]
Given that the induced current ( I ) is 17 µA (17 × 10⁻⁶ A) and the resistance ( R ) is 35 Ω, the induced EMF is:
[ \mathcal{E} = 17 \times 10^{-6}\,\text{A} \times 35\,\Omega = 0.000595\,\text{V} ]
Equating the two expressions for EMF:
[ I \times R = B \times A ]
Solving for ( B ):
[ B = \frac{I \times R}{A} = \frac{0.000595\,\text{V}}{0.0024\,\text{m}^2} \approx 0.2479\,\text{T} ]
Therefore, the magnitude of the magnetic field is approximately 0.248 T.