Use Implicit Differentiation To Find Dy/Dx And D2y/Dx2

Use Implicit Differentiation To Find Dy/Dx And D2y/Dx2

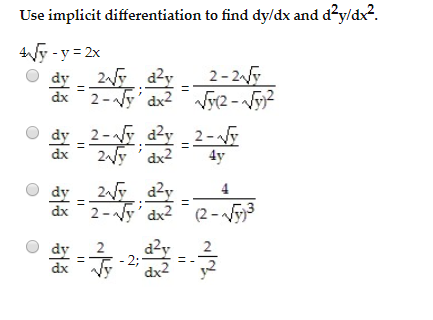
The Correct Answer and Explanation is :

Implicit differentiation is a technique used to find derivatives of functions defined implicitly, where ( y ) is a function of ( x ) but is not explicitly solved for ( y ). This method is particularly useful when dealing with equations that are difficult or impossible to solve explicitly for ( y ).

Finding ( \frac{dy}{dx} ):

Consider the equation ( x^2 + y^2 = 25 ), which represents a circle. To find ( \frac{dy}{dx} ), follow these steps:

1. Differentiate both sides with respect to ( x ):
   [
   \frac{d}{dx}(x^2 + y^2) = \frac{d}{dx}(25)
   ]
   Applying the chain rule to ( y^2 ) (since ( y ) is a function of ( x )):
   [
   2x + 2y \cdot \frac{dy}{dx} = 0
   ]
2. Solve for ( \frac{dy}{dx} ):
   [
   2y \cdot \frac{dy}{dx} = -2x
   ]
   [
   \frac{dy}{dx} = -\frac{x}{y}
   ]

Thus, the derivative of ( y ) with respect to ( x ) is ( \frac{dy}{dx} = -\frac{x}{y} ).

Finding ( \frac{d^2y}{dx^2} ):

To find the second derivative, differentiate ( \frac{dy}{dx} = -\frac{x}{y} ) with respect to ( x ):

1. Differentiate ( \frac{dy}{dx} = -\frac{x}{y} ) with respect to ( x ):
   [
   \frac{d}{dx}\left(-\frac{x}{y}\right) = \frac{d}{dx}\left(\frac{dy}{dx}\right)
   ]
   Using the quotient rule:
   [
   \frac{d^2y}{dx^2} = \frac{(-y)(1) – (-x)\left(\frac{dy}{dx}\right)}{y^2}
   ]
   Substitute ( \frac{dy}{dx} = -\frac{x}{y} ):
   [
   \frac{d^2y}{dx^2} = \frac{-y + x \cdot \left(-\frac{x}{y}\right)}{y^2}
   ]
   Simplify the numerator:
   [
   \frac{d^2y}{dx^2} = \frac{-y – \frac{x^2}{y}}{y^2}
   ]
   Combine terms in the numerator:
   [
   \frac{d^2y}{dx^2} = \frac{-y^2 – x^2}{y^3}
   ]
   Since ( x^2 + y^2 = 25 ), substitute this into the numerator:
   [
   \frac{d^2y}{dx^2} = \frac{-25}{y^3}
   ]

Therefore, the second derivative of ( y ) with respect to ( x ) is ( \frac{d^2y}{dx^2} = -\frac{25}{y^3} ).

Explanation:

Implicit differentiation allows us to differentiate equations where ( y ) is not explicitly expressed as a function of ( x ). By differentiating both sides of the equation with respect to ( x ) and applying the chain rule, we can find ( \frac{dy}{dx} ). To find higher-order derivatives like ( \frac{d^2y}{dx^2} ), we differentiate ( \frac{dy}{dx} ) with respect to ( x ) again, applying the chain rule as needed. This method is particularly useful for curves defined by equations that are difficult to solve explicitly for ( y ).