You have been asked to measure the width of a slit in a piece of paper. You mount the paper 80.0 centimeters from a screen and illuminate it from behind with laser light of wavelength 633 nanometers (in air). You mark two of the intensity minima as shown in the figure, and measure the distance between them to be 17.9millimeters. (Figure 1)
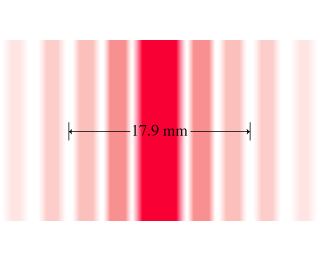
Part A
What is the width a of the slit?
Express your answer in micrometers, to three significant figures.
Part B
If the entire apparatus were submerged in water, would the width of the central peak change?
If the entire apparatus were submerged in water, would the width of the central peak change?
The width would increase.
The width would decrease.
The width would not change.
The Correct Answer and Explanation is :
Part A: Determining the Slit Width
In single-slit diffraction, the angular positions of intensity minima are given by:
asinθm=mλa \sin \theta_m = m \lambda
where:
- aa is the slit width,
- θm\theta_m is the angle to the mm-th minimum,
- mm is the order of the minimum (with m=1m = 1 for the first minimum),
- λ\lambda is the wavelength of the light.
The distance between two adjacent minima on the screen is related to the angle between them by:
Δy=L(θm+1−θm)\Delta y = L (\theta_{m+1} – \theta_m)
where:
- Δy\Delta y is the distance between adjacent minima,
- LL is the distance from the slit to the screen.
For small angles, sinθ≈θ\sin \theta \approx \theta, so the angular separation between adjacent minima is approximately:
θm+1−θm≈λa\theta_{m+1} – \theta_m \approx \frac{\lambda}{a}
Thus, the distance between adjacent minima is:
Δy=Lλa\Delta y = L \frac{\lambda}{a}
Rearranging to solve for aa:
a=LλΔya = \frac{L \lambda}{\Delta y}
Given:
- L=80.0 cm=0.800 mL = 80.0 \, \text{cm} = 0.800 \, \text{m}
- λ=633 nm=633×10−9 m\lambda = 633 \, \text{nm} = 633 \times 10^{-9} \, \text{m}
- Δy=17.9 mm=17.9×10−3 m\Delta y = 17.9 \, \text{mm} = 17.9 \times 10^{-3} \, \text{m}
Substituting these values:
a=0.800×633×10−917.9×10−3a = \frac{0.800 \times 633 \times 10^{-9}}{17.9 \times 10^{-3}}
a≈35.7×10−6 m=35.7 μma \approx 35.7 \times 10^{-6} \, \text{m} = 35.7 \, \mu\text{m}
Therefore, the slit width is approximately 35.7 micrometers.
Part B: Effect of Submerging the Apparatus in Water
When the apparatus is submerged in water, the wavelength of the laser light decreases due to the change in the refractive index. The wavelength in a medium is given by:
λmedium=λvacuumn\lambda_{\text{medium}} = \frac{\lambda_{\text{vacuum}}}{n}
where:
- λvacuum\lambda_{\text{vacuum}} is the wavelength in vacuum,
- nn is the refractive index of the medium.
For water, n≈1.33n \approx 1.33. Therefore, the wavelength in water is:
λwater=633×10−91.33≈476.7×10−9 m\lambda_{\text{water}} = \frac{633 \times 10^{-9}}{1.33} \approx 476.7 \times 10^{-9} \, \text{m}
The angular position of the first minimum in single-slit diffraction is given by:
asinθ1=λmediuma \sin \theta_1 = \lambda_{\text{medium}}
Since aa remains constant and λwater\lambda_{\text{water}} is smaller than λvacuum\lambda_{\text{vacuum}}, the angle θ1\theta_1 decreases. For small angles, sinθ1≈θ1\sin \theta_1 \approx \theta_1, so the position of the first minimum on the screen, y1y_1, is:
y1=Lθ1=Lλmediumay_1 = L \theta_1 = L \frac{\lambda_{\text{medium}}}{a}
Since λmedium\lambda_{\text{medium}} decreases and aa remains constant, y1y_1 decreases. Therefore, the width of the central peak, defined as the distance between the first minima on either side, decreases.
In conclusion, if the entire apparatus were submerged in water, the width of the central peak would decrease.