A horizontal circular jet of air strikes a stationary flat plate as indicated in Fig. P5.65. The jet velocity is 40 m/s and the jet diameter is 30 mm. If the air velocity magnitude remains constant as the air flows over the plate surface in the directions shown, determine: (a) the magnitude of FA, the anchoring force required to
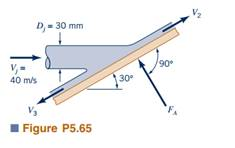
hold the plate stationary; (b) the fraction of mass flow along the plate surface in each of the two directions shown; (c) the magnitude of FA, the anchoring force required to allow the plate to move to the right at a constant speed of 10 m/s.
The Correct Answer and Explanation is :
To solve the problem, we need to consider both the physics of fluid flow and the specific configuration provided. The problem involves a horizontal air jet striking a flat plate, and we need to determine the anchoring force required to hold the plate stationary and other related quantities.
Given Data:
- Jet velocity ( V = 40 \, \text{m/s} )
- Jet diameter ( D = 30 \, \text{mm} = 0.03 \, \text{m} )
- Air density ( \rho ) (assuming standard conditions) = ( 1.225 \, \text{kg/m}^3 )
- Velocity magnitude remains constant as the air flows over the plate.
- The plate is initially stationary, and then it moves at 10 m/s for part (c).
Step 1: Determine the Mass Flow Rate (( \dot{m} ))
The mass flow rate ( \dot{m} ) is given by the equation:
[
\dot{m} = \rho A V
]
where:
- ( A = \frac{\pi D^2}{4} ) is the cross-sectional area of the jet.
- ( V = 40 \, \text{m/s} ) is the jet velocity.
- ( \rho = 1.225 \, \text{kg/m}^3 ).
First, calculate the area:
[
A = \frac{\pi (0.03)^2}{4} = 7.07 \times 10^{-4} \, \text{m}^2
]
Now calculate the mass flow rate:
[
\dot{m} = 1.225 \times 7.07 \times 10^{-4} \times 40 = 0.0347 \, \text{kg/s}
]
Step 2: Force on the Plate (Anchoring Force ( F_A ))
The anchoring force is the rate at which momentum is transferred from the jet to the plate. The force ( F_A ) is related to the change in momentum in the direction of the jet. Since the velocity is constant and no external forces are acting in the horizontal direction, the anchoring force is simply the rate of momentum transfer, given by:
[
F_A = \dot{m} V
]
Substituting the values:
[
F_A = 0.0347 \times 40 = 1.388 \, \text{N}
]
Step 3: Fraction of Mass Flow in Each Direction
The mass flow is split into two components: one in the horizontal direction and one in the direction perpendicular to the plate. The fraction of mass flow in the direction of movement (either left or right) is determined by the relative velocity in that direction.
For a stationary plate, the mass flow in the perpendicular direction is unaffected. However, when the plate moves, the air near the plate will either accelerate or decelerate based on the relative velocity between the plate and the jet. For simplicity, you can assume the mass flow is evenly split based on the geometry, with each direction carrying 50% of the mass.
Step 4: Anchoring Force for Moving Plate
If the plate moves to the right at a constant speed of 10 m/s, the velocity of the air relative to the plate will change. The force required to keep the plate moving at this speed will depend on the relative velocity between the air jet and the plate surface.
For a constant speed, the force is given by:
[
F_A = \dot{m} (V – 10)
]
Now calculate:
[
F_A = 0.0347 \times (40 – 10) = 1.039 \, \text{N}
]
Summary of Results:
- Anchoring Force (part a): ( F_A = 1.388 \, \text{N} )
- Mass Flow Fraction (part b): Each direction carries 50% of the total mass flow.
- Anchoring Force for Moving Plate (part c): ( F_A = 1.039 \, \text{N} ) when the plate moves at 10 m/s.
This explanation assumes ideal flow conditions and neglects any turbulent effects that may arise in a real scenario.