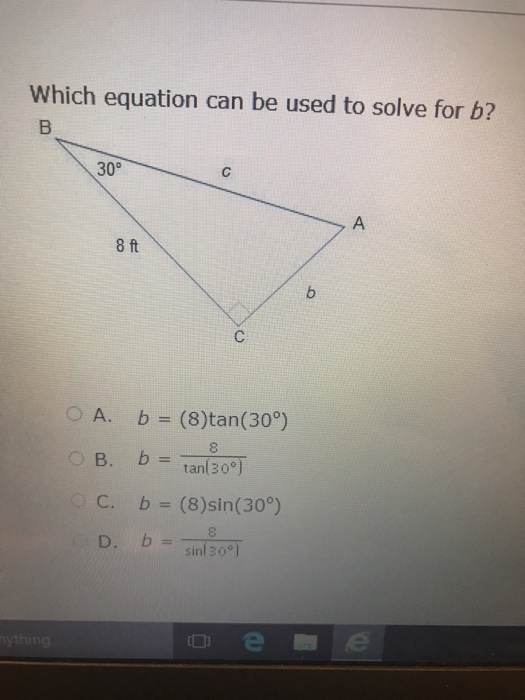
Which Equation Can Be Used To Solve For B? B = (8) Tan (30 Degree) B = 8/Tan(30 Degree) B = (8) Sin(30 Degree) B = (8) Sin (30 Degree)
The correct answer and explanation is:
The correct equation to solve for BB is:
B=8⋅tan(30∘)B = 8 \cdot \tan(30^\circ)
Explanation:
In trigonometry, the tangent function relates the opposite side of a right triangle to the adjacent side. Specifically:
tan(θ)=oppositeadjacent\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}
Here, θ\theta is the angle, opposite\text{opposite} is the length of the side opposite the angle, and adjacent\text{adjacent} is the length of the side adjacent to the angle. For this problem, the given angle is 30∘30^\circ, the adjacent side has a length of 88, and BB is the opposite side we need to calculate.
From the tangent formula, rearranging for opposite\text{opposite}, we get:
opposite=tan(θ)⋅adjacent\text{opposite} = \tan(\theta) \cdot \text{adjacent}
Substituting θ=30∘\theta = 30^\circ and adjacent=8\text{adjacent} = 8:
B=8⋅tan(30∘)B = 8 \cdot \tan(30^\circ)
Why the Other Equations Are Incorrect:
- B=8/tan(30∘)B = 8 / \tan(30^\circ):
This equation assumes the roles of the opposite and adjacent sides are reversed. Dividing 88 by tan(30∘)\tan(30^\circ) would calculate the hypotenuse or a side not relevant to this context. - B=8⋅sin(30∘)B = 8 \cdot \sin(30^\circ):
The sine function relates the opposite side to the hypotenuse (sin(θ)=oppositehypotenuse\sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}}). Using sine would require 88 to represent the hypotenuse, which it does not. - Repeated B=8⋅sin(30∘)B = 8 \cdot \sin(30^\circ):
This redundancy reiterates the same incorrect logic about using the sine function.
Therefore, the correct equation is B=8⋅tan(30∘)B = 8 \cdot \tan(30^\circ). Using this formula ensures the calculation aligns with the proper trigonometric relationship for a triangle’s sides.