A student is standing 20 feet away from the base of a tree. He looks to the top of the tree at a 50 degree angle of elevation. His eyes are 5 feet above the ground. Using cos 50 degrees= 0.64, what is the height of the tree to the nearest foot?
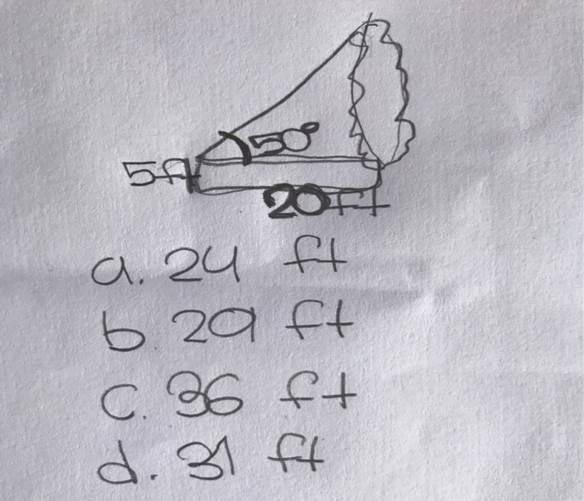
The correct answer and explanation is:
To find the height of the tree, we need to break the problem down into steps. The student is standing 20 feet away from the base of the tree, and he looks up at the top of the tree at a 50-degree angle of elevation. His eyes are 5 feet above the ground, so we need to calculate the height of the tree above his eyes first and then add the 5 feet to account for his height.
Step 1: Set up the right triangle
In this scenario, the height of the tree above the student’s eyes forms the vertical side of a right triangle, and the distance from the student to the base of the tree is the horizontal side (which is 20 feet). The angle of elevation is 50 degrees.
Step 2: Use trigonometry
To calculate the height of the tree above the student’s eyes, we can use the tangent function, which relates the opposite side (height of the tree above his eyes) to the adjacent side (distance from the tree). The tangent of the angle of elevation is the ratio of the height of the tree above the eyes to the horizontal distance from the tree.
We use the formula: tan(θ)=oppositeadjacent\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}
Substitute the known values: tan(50∘)=h20\tan(50^\circ) = \frac{h}{20}
Since tan(50∘)≈1.1918\tan(50^\circ) \approx 1.1918, the equation becomes: 1.1918=h201.1918 = \frac{h}{20}
Now, solve for hh: h=1.1918×20h = 1.1918 \times 20 h≈23.84 feeth \approx 23.84 \text{ feet}
So, the height of the tree above the student’s eyes is approximately 23.84 feet.
Step 3: Add the student’s height
The student’s eyes are 5 feet above the ground, so we add this height to the height of the tree above his eyes: Height of the tree=23.84+5=28.84 feet\text{Height of the tree} = 23.84 + 5 = 28.84 \text{ feet}
To the nearest foot, the height of the tree is approximately 29 feet.
Final Answer:
The height of the tree is 29 feet.