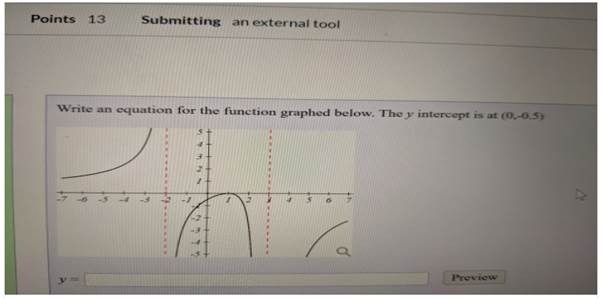
Write an equation for the function graphed below. The y intercept is at (0,-0.5)
The Correct Answer and Explanation is :
To determine the equation of a line with a y-intercept at (0, -0.5), we can utilize the slope-intercept form of a linear equation:
[ y = mx + c ]
Here, ( m ) represents the slope of the line, and ( c ) denotes the y-intercept. Given that the y-intercept is at (0, -0.5), we know ( c = -0.5 ). Therefore, the equation becomes:
[ y = mx – 0.5 ]
To fully define the equation, we need the slope ( m ). The slope indicates the rate at which ( y ) changes with respect to ( x ). Without additional information, such as another point on the line or the slope value, we cannot determine the exact value of ( m ).
For example, if we had another point on the line, say (1, 0), we could calculate the slope using the formula:
[ m = \frac{y_2 – y_1}{x_2 – x_1} ]
Substituting the points (0, -0.5) and (1, 0):
[ m = \frac{0 – (-0.5)}{1 – 0} = \frac{0.5}{1} = 0.5 ]
Thus, the equation of the line would be:
[ y = 0.5x – 0.5 ]
In summary, while we can establish the general form of the equation as [ y = mx – 0.5 ], the exact equation requires knowledge of the slope ( m ), which can be determined if another point on the line is provided.