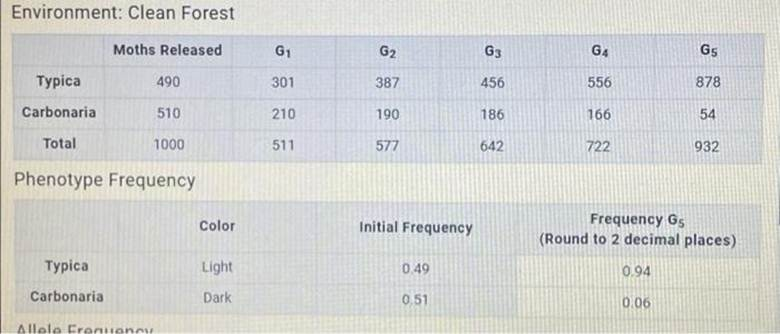
Calculate allele frequencies in the 5th generation. Calculate the genotype frequencies in the 5th generation.
Clean forest
Complete the following steps.
1 Select initial allele frequencies
2 Click Next generation to wait a year for first generation of moths
3 Click Capture moths to monitor population numbers
- Calculate phenotype frequencies in 5th generation. Record in Lab Data
5 Calculate allele frequencies in 5th generation Record in Lab Data
6 Calculate genotype frequencies and number of moths in 5th generation Record in Lab Data
The Correct Answer and Explanation is :

The Correct Answer and Explanation is :
To analyze the evolution of the peppered moth population in a clean forest environment over five generations, we can follow these steps:
1. Initial Allele Frequencies:
Assume the initial frequencies are:
- Dominant allele (D) for dark coloration: 0.10
- Recessive allele (d) for light coloration: 0.90
2. Phenotype Frequencies in the 5th Generation:
In a clean forest, light-colored moths have a survival advantage due to better camouflage against lichen-covered trees. Over successive generations, natural selection favors the light phenotype. By the 5th generation, the population predominantly consists of light-colored moths. For instance, if we observe 913 moths, 857 might be light (Typica) and 56 dark (Carbonaria).
3. Calculating Allele Frequencies in the 5th Generation:
Using the Hardy-Weinberg principle:
- Frequency of light phenotype (typica) = 857 / 913 ≈ 0.94
- Assuming typica is homozygous recessive (dd), then q² = 0.94
- q (frequency of allele d) = √0.94 ≈ 0.97
- p (frequency of allele D) = 1 – q = 1 – 0.97 = 0.03
4. Calculating Genotype Frequencies in the 5th Generation:
Applying Hardy-Weinberg equilibrium:
- Frequency of DD (homozygous dominant) = p² = (0.03)² ≈ 0.0009
- Frequency of Dd (heterozygous) = 2pq = 2 * 0.03 * 0.97 ≈ 0.058
- Frequency of dd (homozygous recessive) = q² = (0.97)² ≈ 0.94
5. Number of Moths per Genotype in the 5th Generation:
Given a total population of 913 moths:
- DD: 0.0009 * 913 ≈ 1 moth
- Dd: 0.058 * 913 ≈ 53 moths
- dd: 0.94 * 913 ≈ 859 moths
Explanation:
The peppered moth (Biston betularia) exhibits two primary color morphs: light (typica) and dark (carbonaria). The coloration is genetically determined, with the dark phenotype being dominant (allele D) and the light phenotype recessive (allele d). In environments where tree bark is light due to lichen cover, light-colored moths have a camouflage advantage, reducing predation by birds. Conversely, in polluted areas where soot darkens tree bark, dark-colored moths are better camouflaged.
In a clean forest setting, natural selection favors the light-colored moths. Over successive generations, the frequency of the d allele increases, leading to a higher proportion of light-colored moths. By the 5th generation, as calculated, the d allele frequency approaches 0.97, and the D allele frequency decreases to approximately 0.03. This shift results in a population where about 94% of the moths are light-colored (dd genotype).
These calculations align with the principles of natural selection, where environmental pressures influence allele frequencies within a population. The peppered moth serves as a classic example of this process, demonstrating how species can rapidly adapt to changes in their environment.