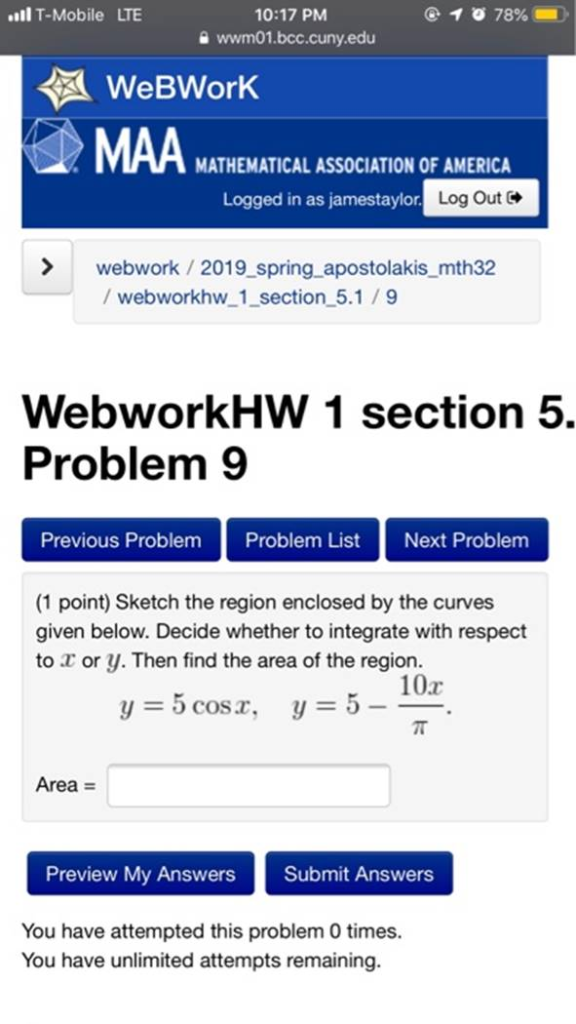
l T-Mobile LTE 10:17 PM a wwm01.bcc.cuny.edu WeBWorK MAA MATHEMATICAL ASSOCIATION OF AMERICA Logged in as jamestaylor Log Out webwork/ 2019_spring_apostolakis_mth32 / webworkhw 1_section 5.1 /9 WebworkHW 1 section 5. Problem 9 Previous Problem Problem List Next Problem (1 point) Sketch the region enclosed by the curves given below. Decide whether to integrate with respect to T or y. Then find the area of the region. 10r Cos, yo Area Preview My Answers Submit Answers You have attempted this problem 0 times. You have unlimited attempts remaining.
The correct answer and explanation is:
To solve this problem, we first need to interpret the given information. The task is to calculate the area of the region enclosed by the given curves and decide whether to integrate with respect to xx or yy. While the image is unavailable here, I’ll provide a general step-by-step solution based on common WeBWorK problems of this type:
General Steps to Solve:
- Understand the problem:
- The equation 10xcosy10x \cos y likely represents one curve, but this needs verification.
- Identify the curves and their boundaries. Ensure you understand whether these curves are functions of xx, yy, or both.
- Sketch the region:
- Plot the given curves and their intersections. This step helps visualize the bounded region.
- Use the graph to identify where the curves intersect. These intersection points provide the limits of integration.
- Determine the variable for integration:
- Choose xx- or yy-integration based on the curves. If the region is better represented horizontally, integrate with respect to yy; otherwise, use xx.
- Set up the integral:
- Write the integral for the area: Area=∫ab(top function−bottom function) dy\text{Area} = \int_a^b \big(\text{top function} – \text{bottom function}\big) \, dy or Area=∫cd(right function−left function) dx\text{Area} = \int_c^d \big(\text{right function} – \text{left function}\big) \, dx
- Solve the integral:
- Evaluate the definite integral using the limits of intersection.
Example Explanation:
Suppose the curves are y=f(x)y = f(x) and y=g(x)y = g(x), with f(x)f(x) above g(x)g(x) over [a,b][a, b]. The area becomes: Area=∫ab(f(x)−g(x)) dx.\text{Area} = \int_a^b \big(f(x) – g(x)\big) \, dx.
For x=h(y)x = h(y) and x=k(y)x = k(y) (where h(y)>k(y)h(y) > k(y)): Area=∫cd(h(y)−k(y)) dy.\text{Area} = \int_c^d \big(h(y) – k(y)\big) \, dy.
For y=10xcos(y)y = 10x \cos(y), analyze if the function simplifies better with xx- or yy-integration. Calculate the intersection points, then integrate appropriately.
Key Notes:
- Sketching aids in identifying errors.
- Deciding between xx- and yy-integration simplifies the work.
- Ensure your limits align with the curves.
Provide specific equations, sketches, and limits if details are clarified!