In the discussion of the Lindemann mechanism, it was assumed that the rate of activation by collision with another reactant molecule A was the same as collision with a nonreactant molecule M such as a buffer gas. What if the rates of activation for these two processes are different? In this case, the mechanism becomes
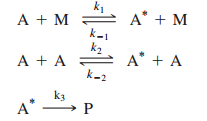
a. Demonstrate that the rate law expression for this mechanism is
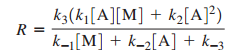
b. Does this rate law reduce to the expected form when [M] = 0?
The Correct Answer and Explanation is :
To analyze the given Lindemann mechanism where the rates of activation for the reactant molecule AA and the buffer gas MM differ, we derive the rate law step-by-step.
Mechanism:
- A+M⇌k−1k1A∗+MA + M \xrightleftharpoons[k_{-1}]{k_1} A^* + M (Activation of AA by MM)
- A+A⇌k−2k2A∗+AA + A \xrightleftharpoons[k_{-2}]{k_2} A^* + A (Activation of AA by AA)
- A∗→k3productsA^* \xrightarrow{k_3} \text{products} (Deactivation and product formation)
Here, A∗A^* is the activated intermediate.
Derivation:
The steady-state approximation is applied to A∗A^*, assuming its concentration does not change significantly during the reaction. d[A∗]dt=0=k1[A][M]+k2[A][A]−k−1[A∗][M]−k−2[A∗][A]−k3[A∗]\frac{d[A^*]}{dt} = 0 = k_1[A][M] + k_2[A][A] – k_{-1}[A^*][M] – k_{-2}[A^*][A] – k_3[A^*]
Rearranging for [A∗][A^*]: [A∗]=k1[A][M]+k2[A][A]k−1[M]+k−2[A]+k3[A^*] = \frac{k_1[A][M] + k_2[A][A]}{k_{-1}[M] + k_{-2}[A] + k_3}
The rate of product formation (RR) is given by: R=k3[A∗]R = k_3[A^*]
Substituting [A∗][A^*]: R=k3(k1[A][M]+k2[A][A])k−1[M]+k−2[A]+k3R = \frac{k_3 \big( k_1[A][M] + k_2[A][A] \big)}{k_{-1}[M] + k_{-2}[A] + k_3}
This is the rate law for the mechanism.
Special Case: [M]=0[M] = 0
When [M]=0[M] = 0: R=k3⋅k2[A][A]k−2[A]+k3R = \frac{k_3 \cdot k_2[A][A]}{k_{-2}[A] + k_3}
Factoring AA out: R=k2k3[A]2k−2[A]+k3R = \frac{k_2k_3[A]^2}{k_{-2}[A] + k_3}
This aligns with the expected Lindemann-Hinshelwood mechanism for unimolecular reactions in the absence of a buffer gas.
Explanation:
This derivation demonstrates that incorporating different rates for activation by MM and AA results in a more complex rate law, blending contributions from both reactant and buffer. When [M]=0[M] = 0, the system naturally reduces to a form dependent solely on AA, as expected for reactions without a buffer. This dual dependence allows for flexibility in modeling real systems where buffer gases influence activation differently.