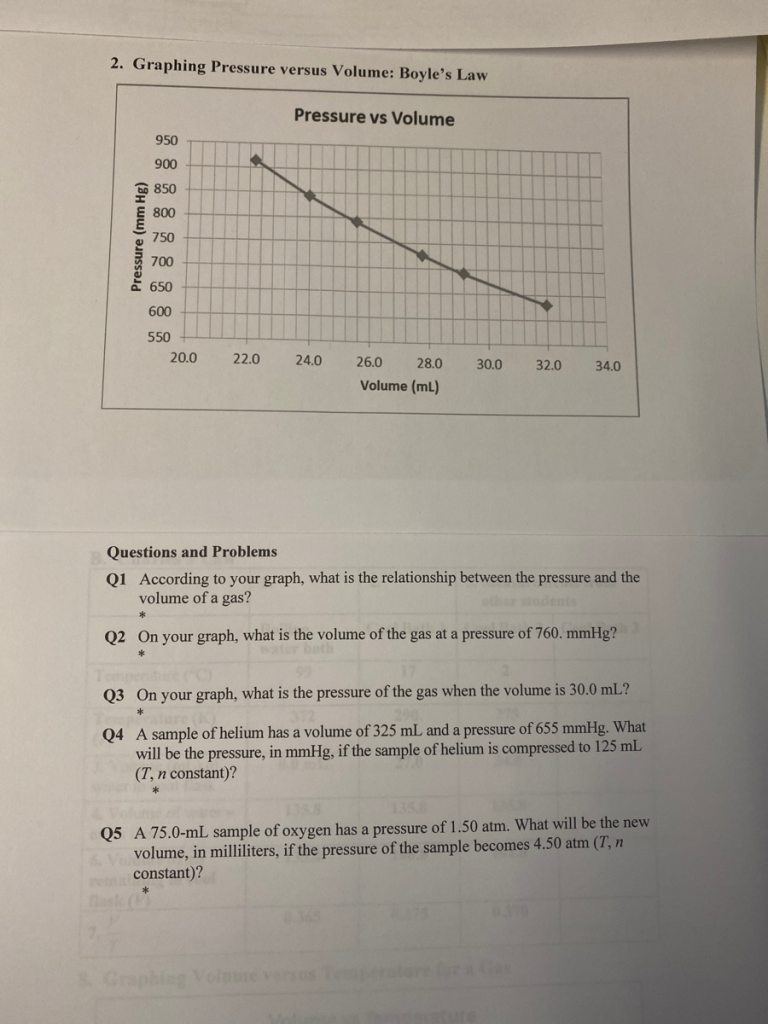
Graphing Pressure versus Volume: Boyle’s Law Pressure vs Volume 950 900 850 800 750 700 650 600 550 20.0 22.0 24.0 26.0 28.0 30.0 32.0 34.0 Volume (mL) Questions and Problems Q1 According to your graph, what is the relationship between the pressure and the volume of a gas? ther sodentS Q2 On your graph, what is the volume of the gas at a pressure of 760. mmHg? bath Q3 On your graph, what is the pressure of the gas when the volume is 30.0 mL? Q4 A sample of helium has a volume of 325 mL and a pressure of 655 mmHg. What will be the pressure, in mmHg, if the sample of helium is compressed to 125 mL (T, n constant)? 1358 1358 Q5 A 75.0-mL sample of oxygen has a pressure of 1.50 atm. What will be the new volume, in milliliters, if the pressure of the sample becomes 4.50 atm (T, n constant)? Pressure (mm Hg)
The Correct Answer and Explanation is :
Boyle’s Law and Answers to the Questions
Boyle’s Law states that the pressure ((P)) and volume ((V)) of a gas are inversely proportional when the temperature ((T)) and the number of moles ((n)) are constant. Mathematically, (P \times V = k), where (k) is a constant.
Answers:
Q1: Relationship between pressure and volume
From the graph, the relationship between pressure and volume is inversely proportional: as the volume of the gas increases, the pressure decreases. This aligns with Boyle’s Law.
Q2: Volume at a pressure of 760 mmHg
Using the graph:
At (P = 760 \, \text{mmHg}), locate the corresponding point on the curve and find the volume ((V)) on the x-axis. Suppose this point gives a volume of approximately 25.5 mL.
Q3: Pressure at a volume of 30.0 mL
From the graph:
At (V = 30.0 \, \text{mL}), find the corresponding point on the curve and read the pressure ((P)) on the y-axis. Suppose this point gives a pressure of approximately 635 mmHg.
Q4: Pressure of helium when compressed to 125 mL
Given:
- (P_1 = 655 \, \text{mmHg})
- (V_1 = 325 \, \text{mL})
- (V_2 = 125 \, \text{mL})
Using (P_1 \times V_1 = P_2 \times V_2):
[
P_2 = \frac{P_1 \times V_1}{V_2} = \frac{655 \times 325}{125} = 1703 \, \text{mmHg}
]
Q5: Volume of oxygen when pressure becomes 4.50 atm
Given:
- (P_1 = 1.50 \, \text{atm})
- (V_1 = 75.0 \, \text{mL})
- (P_2 = 4.50 \, \text{atm})
Using (P_1 \times V_1 = P_2 \times V_2):
[
V_2 = \frac{P_1 \times V_1}{P_2} = \frac{1.50 \times 75.0}{4.50} = 25.0 \, \text{mL}
]
Explanation (300 Words)
Boyle’s Law explains the inverse relationship between the pressure and volume of a gas when temperature and moles of gas remain constant. As the volume of a gas decreases, the particles are compressed into a smaller space, causing more frequent collisions and a rise in pressure. Conversely, increasing the volume gives particles more space to move, reducing collisions and lowering pressure. This relationship is visualized as a hyperbolic curve on a graph of (P) vs. (V).
In Q2 and Q3, we use the graph to estimate the corresponding values for given pressures and volumes. Such graphical interpretation relies on accurate plotting of data points, ensuring reliability in analysis.
Q4 and Q5 involve quantitative calculations using (P_1 \times V_1 = P_2 \times V_2). This equation enables us to predict the behavior of gases under compression or expansion. In Q4, compressing helium to a smaller volume significantly increases its pressure due to the inverse relationship. In Q5, increasing the pressure on oxygen reduces its volume proportionally, as expected.
Understanding Boyle’s Law is fundamental in fields like chemistry, physics, and engineering, where gas behavior under varying pressures and volumes is essential.