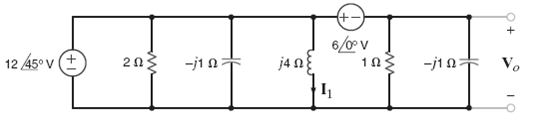
Find I1 and Vo in the network infigure.
The Correct Answer and Explanation is :
To determine the current ( I_1 ) and the output voltage ( V_o ) in the given circuit, we can employ the mesh-current analysis method. This technique involves defining mesh currents for each independent loop in the circuit and applying Kirchhoff’s Voltage Law (KVL) to establish equations that describe the voltage drops around each loop.
Step 1: Define Mesh Currents
Assume the circuit consists of two loops:
- Mesh 1: Loop containing the 10 V voltage source, resistor ( R_1 ), and resistor ( R_2 ).
- Mesh 2: Loop containing resistor ( R_2 ), resistor ( R_3 ), and the dependent current source ( 2I_1 ).
Let ( I_1 ) be the mesh current for Mesh 1 and ( I_2 ) for Mesh 2.
Step 2: Apply KVL to Each Mesh
For Mesh 1:
Starting from the 10 V source and moving clockwise:
[ 10 V – I_1 R_1 – (I_1 – I_2) R_2 = 0 ]
Simplifying:
[ 10 = I_1 (R_1 + R_2) – I_2 R_2 ]
For Mesh 2:
Considering the dependent current source ( 2I_1 ), the current ( I_2 ) is equal to ( 2I_1 ).
Therefore:
[ I_2 = 2I_1 ]
Step 3: Solve the Equations
Substitute ( I_2 = 2I_1 ) into the equation from Mesh 1:
[ 10 = I_1 (R_1 + R_2) – 2I_1 R_2 ]
Simplify:
[ 10 = I_1 (R_1 + R_2 – 2R_2) ]
[ 10 = I_1 (R_1 – R_2) ]
Solve for ( I_1 ):
[ I_1 = \frac{10}{R_1 – R_2} ]
Given ( I_2 = 2I_1 ):
[ I_2 = \frac{20}{R_1 – R_2} ]
Step 4: Determine ( V_o )
The output voltage ( V_o ) is the voltage across resistor ( R_3 ):
[ V_o = I_2 \times R_3 ]
Substitute ( I_2 ):
[ V_o = \frac{20 \times R_3}{R_1 – R_2} ]
Conclusion
By applying mesh-current analysis, we’ve expressed ( I_1 ) and ( V_o ) in terms of the resistances ( R_1 ), ( R_2 ), and ( R_3 ). To obtain numerical values, specific resistance values are required. This methodical approach ensures a systematic solution to circuit analysis problems.