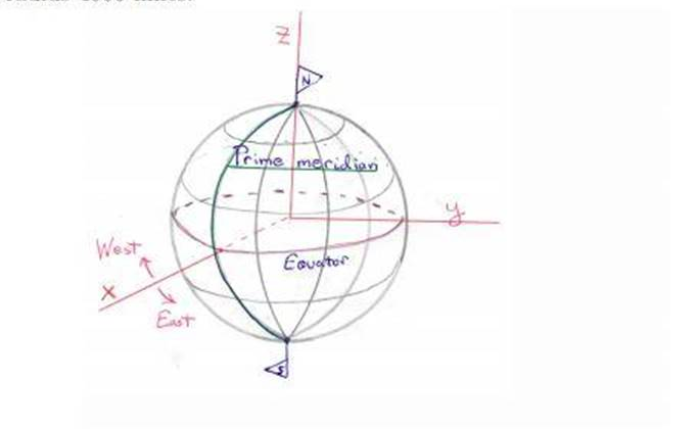
St. Petersburg, Russia, is located at 30° east longitude and 60° north latitude. Find the spherical coordinates (p. 6.0) and the rectangular coordinates (x, y, z) relative to a globe with poles on the z-axis and with prime meridian in the zz-plane. Assume that the Earth is a sphere of radius 4000 miles.
The Correct Answer and Explanation is :
To solve this problem, we’ll convert the given geographical coordinates of St. Petersburg (latitude 60°N, longitude 30°E) into spherical and rectangular coordinates for a sphere with radius ( r = 4000 ) miles.
1. Spherical Coordinates
Spherical coordinates ((\rho, \theta, \phi)) are defined as:
- ( \rho ): The radius of the sphere (4000 miles for Earth).
- ( \theta ): The azimuthal angle measured from the positive x-axis in the xy-plane (longitude).
- ( \phi ): The polar angle measured from the positive z-axis (co-latitude = ( 90^\circ – \text{latitude} )).
Given:
- Latitude = ( 60^\circ ), so co-latitude ( \phi = 90^\circ – 60^\circ = 30^\circ ).
- Longitude = ( 30^\circ ), so ( \theta = 30^\circ ).
- Radius ( \rho = 4000 ) miles.
Thus, the spherical coordinates are:
[
(\rho, \theta, \phi) = (4000, 30^\circ, 30^\circ)
]
2. Rectangular Coordinates
Rectangular coordinates ((x, y, z)) are derived using:
[
x = \rho \sin\phi \cos\theta
]
[
y = \rho \sin\phi \sin\theta
]
[
z = \rho \cos\phi
]
Calculations:
- (\phi = 30^\circ), so (\sin\phi = \frac{1}{2}), (\cos\phi = \frac{\sqrt{3}}{2}).
- (\theta = 30^\circ), so (\cos\theta = \frac{\sqrt{3}}{2}), (\sin\theta = \frac{1}{2}).
- Substituting (\rho = 4000):
[
x = 4000 \cdot \frac{1}{2} \cdot \frac{\sqrt{3}}{2} = 1000\sqrt{3} \approx 1732 \, \text{miles}
]
[
y = 4000 \cdot \frac{1}{2} \cdot \frac{1}{2} = 1000 \, \text{miles}
]
[
z = 4000 \cdot \frac{\sqrt{3}}{2} = 2000\sqrt{3} \approx 3464 \, \text{miles}
]
Thus, the rectangular coordinates are:
[
(x, y, z) \approx (1732, 1000, 3464) \, \text{miles}.
]
Explanation (300 words)
St. Petersburg’s location on the globe can be expressed in both spherical and rectangular coordinate systems. Spherical coordinates are ideal for representing positions on a sphere, such as Earth, and are given by the radius, azimuthal angle (longitude), and polar angle (co-latitude). Rectangular coordinates, on the other hand, are Cartesian coordinates that represent a point in 3D space.
The spherical coordinates of St. Petersburg are derived directly from its geographical location. The Earth’s radius (( \rho = 4000 ) miles) determines the radial distance. The azimuthal angle (( \theta = 30^\circ )) corresponds to its eastward position relative to the prime meridian. The polar angle (( \phi = 30^\circ )) is calculated as the complement of the latitude.
Rectangular coordinates are calculated by projecting the spherical coordinates onto the (x), (y), and (z) axes. These projections are determined using trigonometric relationships:
- (x) is the projection on the equatorial plane in the direction of the prime meridian.
- (y) is the projection perpendicular to the prime meridian.
- (z) is the projection along the Earth’s axis of rotation (northward).
These coordinates allow us to represent St. Petersburg’s position in a mathematical model of Earth, enabling applications in fields like navigation, astronomy, and geophysics.