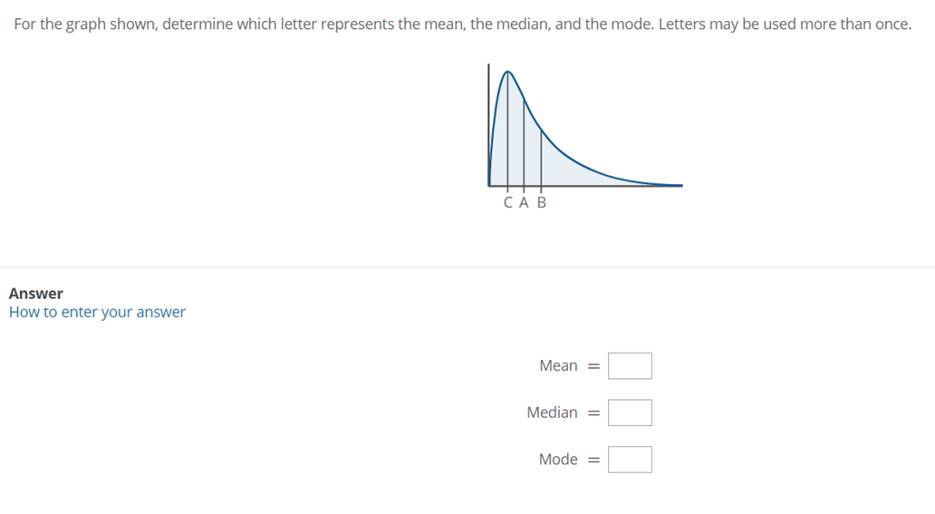
For the graph shown, determine which letter represents the mean, the median, and the mode. Letters may be used more than once. CAB Answer How to enter your answer Mean- Median Mode The following data represent the number of oranges, in hundreds, which were sold by various grocery stores in the month of May. Construct a dot plot for the given data. 11 9 13 11 14 13 15 6 6 6 9 4 2 12 15 1 Copy Data Answer Tables Keypad Select any value to see the controls for increasing or decreasing the frequency. Use the up and down arrows or drag the slider to change the number of dots. 0 2 3 4 5 6 789 10 11 12 13 14 15 16 Use your knowledge of pie charts to answer the following questions. Step 1 of 2 : The total of all the frequencies in a frequency table is 206. If a section in a pie chart corresponds to an item with a frequency of 61, what is the size of the angle of the corresponding circular wedge? Round your answer to the nearest degree. Tables Keypad Answer How to enter your answer Consider the following frequency table representing the distribution of cost of lunch (in dollars) Cost of Lunch (in Dollars) Class 7.6-8.3 8.4-9.1 9.2-9.9 10.0-10.7 10.8-11.5 Frequency 10 13 Step 1 of 2: Determine the cumulative frequency for the fifth class.


The Correct Answer and Explanation is :
Let’s break down the questions one by one.
1. Mean, Median, and Mode from a Graph (Letters representing the values)
Unfortunately, I cannot view the graph that you’re referring to. However, I can explain how you would typically determine which letter corresponds to the mean, median, and mode:
- Mean: The mean is the arithmetic average of the data points. It’s calculated by adding all the numbers and then dividing by the total number of data points.
- Median: The median is the middle value when the data points are arranged in order. If there’s an odd number of data points, it’s the middle one; if there’s an even number, it’s the average of the two middle values.
- Mode: The mode is the value that appears most frequently in the data set.
If you’re referring to a dot plot where each dot represents a data point, you can identify the mean, median, and mode based on the distribution of dots on the plot. The mode will be the value with the highest stack of dots, the median will be the value in the middle of the distribution, and the mean will be around the center of the distribution (but might not align exactly with the median if the data is skewed).
2. Dot Plot for Oranges Sold in May
The data given: 11, 9, 13, 11, 14, 13, 15, 6, 6, 6, 9, 4, 2, 12, 15, 1.
To construct a dot plot:
- Place each value on a number line from 1 to 15.
- For each occurrence of a value, place a dot above the corresponding number.
Example: For the number 6, since it appears three times, place three dots above the number 6.
The resulting dot plot will have the following frequency of dots:
- 1: 1 dot
- 2: 1 dot
- 4: 1 dot
- 6: 3 dots
- 9: 2 dots
- 11: 2 dots
- 12: 1 dot
- 13: 2 dots
- 14: 1 dot
- 15: 2 dots
This should give you a visual representation of the data.
3. Pie Chart Angle Calculation
The total frequency is 206, and one section of the pie chart corresponds to an item with a frequency of 61.
To find the angle of the corresponding wedge:
- The formula for the angle of a wedge in a pie chart is:
[
\text{Angle of wedge} = \left( \frac{\text{Frequency of the item}}{\text{Total frequency}} \right) \times 360^\circ
]
Plugging in the numbers:
[
\text{Angle} = \left( \frac{61}{206} \right) \times 360^\circ = 106.59^\circ
]
Rounding to the nearest degree gives 107°.
4. Cumulative Frequency
For the frequency table provided with lunch costs:
| Cost of Lunch (in dollars) | Frequency |
|---|---|
| 7.6 – 8.3 | 10 |
| 8.4 – 9.1 | 13 |
| 9.2 – 9.9 | ? |
| 10.0 – 10.7 | ? |
| 10.8 – 11.5 | ? |
The cumulative frequency is the sum of the frequencies as we go down the table:
- For the 1st class: cumulative frequency = 10
- For the 2nd class: cumulative frequency = 10 + 13 = 23
- For the 3rd class: cumulative frequency = 23 + ?
- For the 4th class: cumulative frequency = 23 + ?
- For the 5th class: cumulative frequency = 23 + ?
You can calculate the cumulative frequency for the entire table based on the actual frequency values.
Hope this clears up your questions! Let me know if you’d like further details or have any other questions.