Department of Mathematics Course Help Hw19 Obj C4: Problem 5 Previous Problem List Next (1 point) Find the exponential function f(x)-a.b whose graph is shown below 13.6) Preview My Answers Submit Answers Page generated at 10/17/2018 at 01 58am EDT
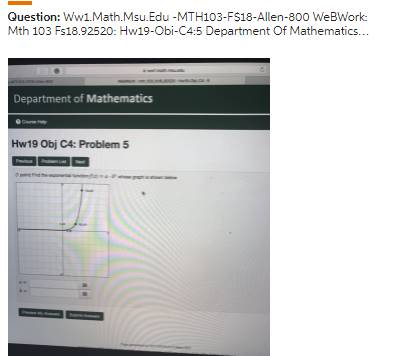
The Correct Answer and Explanation is :
To determine the exponential function ( f(x) = a \cdot b^x ) that matches the provided graph, we need to analyze the graph’s key features, such as the initial value and the growth rate. The parameter ( a ) represents the initial value of the function when ( x = 0 ), and ( b ) is the base that dictates the growth rate.
Step 1: Identify the Initial Value
The initial value ( a ) is the value of ( f(x) ) when ( x = 0 ). From the graph, observe the point where the curve intersects the y-axis (i.e., when ( x = 0 )). This point provides the value of ( a ).
Step 2: Determine the Growth Rate
The base ( b ) determines how the function grows as ( x ) increases. If the graph shows exponential growth, ( b ) will be greater than 1; if it shows exponential decay, ( b ) will be between 0 and 1. To find ( b ), select two points on the graph with known coordinates. Let these points be ( (x_1, y_1) ) and ( (x_2, y_2) ). Using the general form of the exponential function, we have:
[ y_1 = a \cdot b^{x_1} ]
[ y_2 = a \cdot b^{x_2} ]
Dividing the second equation by the first eliminates ( a ):
[ \frac{y_2}{y_1} = \frac{a \cdot b^{x_2}}{a \cdot b^{x_1}} = b^{x_2 – x_1} ]
Taking the natural logarithm of both sides:
[ \ln\left( \frac{y_2}{y_1} \right) = (x_2 – x_1) \cdot \ln(b) ]
Solving for ( \ln(b) ):
[ \ln(b) = \frac{\ln\left( \frac{y_2}{y_1} \right)}{x_2 – x_1} ]
Finally, exponentiating both sides gives ( b ):
[ b = \exp\left( \frac{\ln\left( \frac{y_2}{y_1} \right)}{x_2 – x_1} \right) ]
Step 3: Construct the Exponential Function
With ( a ) and ( b ) determined, the exponential function is:
[ f(x) = a \cdot b^x ]
Example:
Suppose the graph shows that when ( x = 0 ), ( f(x) = 3 ) (so ( a = 3 )), and when ( x = 2 ), ( f(x) = 12 ). Using the formula for ( b ):
[ b = \exp\left( \frac{\ln\left( \frac{12}{3} \right)}{2 – 0} \right) = \exp\left( \frac{\ln(4)}{2} \right) = \exp\left( \frac{2 \ln(2)}{2} \right) = \exp(\ln(2)) = 2 ]
Therefore, the exponential function is:
[ f(x) = 3 \cdot 2^x ]
This function starts at 3 when ( x = 0 ) and doubles every time ( x ) increases by 1, matching the observed growth rate.
For a visual explanation of graphing exponential functions, you might find the following video helpful: