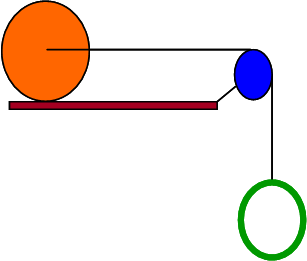
An green hoop with mass mh = 2.4 kg and radius R = 0.14 m hangs from a string that goes over a blue solid disk pulley with mass md = 2.3 kg and radius Rd= 0.08 m. The other end of the string is attached to a massless axel through the center of an orange sphere on a flat horizontal surface that rolls without slipping and has mass ms = 3.7 kg and radius Rs = 0.23 m. The system is released from rest.
1) What is magnitude of the linear acceleration of the hoop?
2) What is the magnitude of the angular acceleration of the sphere?
3) What is the tension in the string between the sphere and disk pulley?
The Correct Answer and Explanation is :
It seems I’m unable to access the image you’ve linked. However, I can still help with your physics question regarding the motion of the system described.
Problem Breakdown:
We have a system with a hoop, disk pulley, and sphere, all connected by a string, and the system is released from rest. We’ll approach each part step by step.
1. Linear acceleration of the hoop:
To find the linear acceleration of the hoop, we need to consider the forces acting on the hoop, its moment of inertia, and the relationship between angular and linear acceleration. Since there is a string connecting the hoop and the disk, the tensions in the string are essential.
- The hoop’s moment of inertia IhI_h for a thin ring is given by: Ih=mhRh2I_h = m_h R_h^2 where mhm_h is the mass of the hoop and RhR_h is its radius.
- Using Newton’s second law, the force on the hoop will be influenced by the tension TT in the string, and the hoop will have both translational and rotational motion. The force on the hoop will give us the linear acceleration aha_h.
We use the equation: T=mhahT = m_h a_h
The rotational version of Newton’s second law for the hoop is: TRh=IhαhT R_h = I_h \alpha_h
where αh\alpha_h is the angular acceleration of the hoop, and the relationship between linear and angular acceleration is ah=αhRha_h = \alpha_h R_h.
From these two equations, we can solve for the acceleration aha_h.
2. Angular acceleration of the sphere:
The sphere rolls without slipping, so its linear acceleration asa_s and angular acceleration αs\alpha_s are related by: as=Rsαsa_s = R_s \alpha_s
The forces acting on the sphere include the tension in the string, which leads to the torque causing angular acceleration.
The moment of inertia for the sphere is: Is=25msRs2I_s = \frac{2}{5} m_s R_s^2
Applying Newton’s second law for rotation: TsRs=IsαsT_s R_s = I_s \alpha_s
where TsT_s is the tension on the string connected to the sphere.
Using the relation as=Rsαsa_s = R_s \alpha_s, we can solve for αs\alpha_s.
3. Tension in the string between the sphere and disk pulley:
Finally, the tension in the string between the sphere and the disk pulley can be found by considering the rotational and linear dynamics of the disk. The tension TdT_d will be influenced by the disk’s moment of inertia and its rotational acceleration. The tension between the sphere and the disk pulley can be related to the other tensions in the system.
To summarize, the steps to solving this problem involve writing the equations for the forces and torques on each object (hoop, disk, and sphere) and solving the system of equations that describes their motion.