Graphing Radical Functions

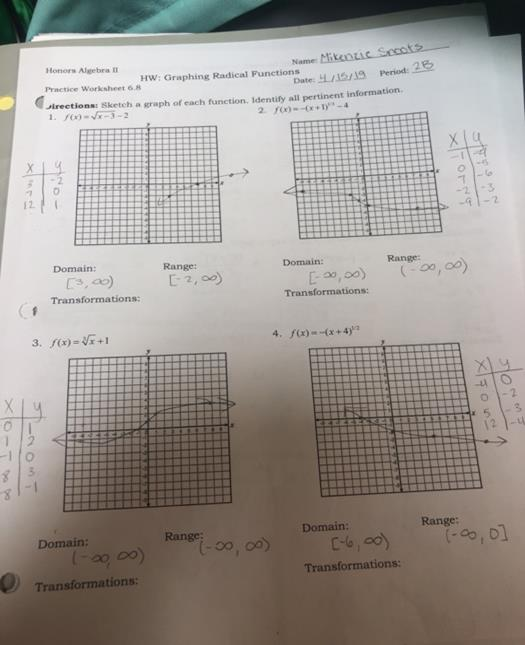
Sketch a graph of each function. Identify all pertinent information HW: Graphing Radical Functions a/159Period: 28 2, f(x)s-(x +1尸-4 32 フ 0 12 2 Domain: Range: Domain: 00, 00 Cs, ao) Transformations: Transformations: 3. f(x)- +1 0 5 12 Domain: Range: Domain: Range:

The Correct Answer and Explanation is :

It looks like you’re asking for help with graphing and analyzing radical functions. Let’s break down the functions and provide a detailed explanation for each.

Function 1: ( f(x) = -\sqrt{x + 1} – 4 )

1. Domain:
   The expression inside the square root must be non-negative, so:
   [
   x + 1 \geq 0 \quad \Rightarrow \quad x \geq -1
   ]
   Therefore, the domain of this function is ( x \in [-1, \infty) ).
2. Range:
   The square root function produces non-negative values, but since it’s multiplied by -1, the values will be non-positive. Additionally, the function shifts down by 4 units. Therefore, the range of this function is:
   [
   y \in (-\infty, -4]
   ]
3. Transformations:

• The negative sign in front of the square root reflects the graph across the x-axis.
• The “+1” inside the square root shifts the graph to the left by 1 unit.
• The “-4” outside the square root shifts the graph down by 4 units.

Function 2: ( f(x) = \sqrt{x – 5} + 12 )

1. Domain:
   The expression inside the square root must be non-negative, so:
   [
   x – 5 \geq 0 \quad \Rightarrow \quad x \geq 5
   ]
   Therefore, the domain of this function is ( x \in [5, \infty) ).
2. Range:
   The square root function produces non-negative values, and the “+12” outside the square root shifts the graph up by 12 units. Therefore, the range of this function is:
   [
   y \in [12, \infty)
   ]
3. Transformations:

• The “+5” inside the square root shifts the graph to the right by 5 units.
• The “+12” outside the square root shifts the graph up by 12 units.

Visual Graphing:

While I can’t draw the graph directly here, I can help you create the graph of both functions by plotting them using graphing software or a graphing calculator.

To summarize:

• Function 1 is a transformed square root function with a reflection, left shift, and downward shift.
• Function 2 is a square root function with a rightward shift and an upward shift.

These transformations affect both the domain and range of the functions, which is crucial for graphing. Make sure to plot each point carefully and observe how the shifts and reflections affect the shape and position of the graph.

If you need further help graphing these functions, feel free to ask!