Identify the Westgard rules the following Levey-Jennings charts violate on days 12 and 20. Tell whether each violation implies a random or systematic error.
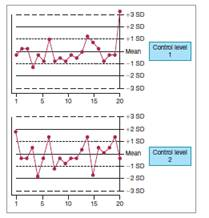
The Correct Answer and Explanation is :
The Levey-Jennings charts for days 12 and 20 exhibit violations of specific Westgard rules, each indicative of different types of errors:
Day 12: Violation of the 1_3s Rule
- Rule Violated: 1_3s
- Description: This rule is violated when a single control measurement exceeds the mean plus 3 standard deviations (3σ) or the mean minus 3σ.
- Implication: A violation of the 1_3s rule suggests the presence of random error.
- Explanation: Random errors are unpredictable and can cause occasional outliers. A single data point exceeding the 3σ limit indicates an isolated incident of random error, which is typically not systematic and does not affect the overall accuracy of the measurement system.
Day 20: Violation of the 2_2s Rule
- Rule Violated: 2_2s
- Description: This rule is violated when two consecutive control measurements exceed the same mean plus 2σ or the same mean minus 2σ.
- Implication: A violation of the 2_2s rule indicates a systematic error.
- Explanation: Systematic errors cause consistent deviations in measurements, leading to a shift in the mean. Two consecutive points exceeding the 2σ limit on the same side of the mean suggest a persistent bias in the measurement system, which could be due to factors such as reagent degradation, instrument calibration drift, or environmental changes affecting the measurement process.
Understanding Westgard Rules and Error Types
Westgard rules are statistical guidelines used in quality control to monitor the performance of analytical processes. They help distinguish between random and systematic errors:
- Random Errors: These are unpredictable fluctuations that cause occasional outliers. They are typically detected by rules like 1_3s and R_4s.
- Systematic Errors: These are consistent biases that affect all measurements in a particular direction. They are often identified by rules such as 2_2s, 4_1s, and 10_x.
By applying these rules, laboratories can maintain the accuracy and reliability of their analytical measurements, ensuring that patient results are both precise and accurate.