What is the approximate diameter of
the nucleus in units of pm?
The Correct Answer and Explanation is :
The diameter of an atomic nucleus is approximately 10 to 15 femtometers (fm), which is equivalent to 10,000 to 15,000 picometers (pm). (en.wikipedia.org)
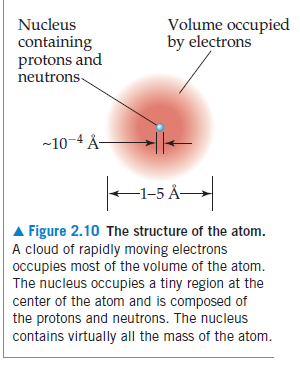
Understanding Atomic Nucleus Size
The atomic nucleus, composed of protons and neutrons, is the dense central core of an atom. Its size is significantly smaller than that of the entire atom, which includes the electron cloud. While the atom’s diameter is on the order of 200 pm, the nucleus’s diameter is about 10,000 times smaller, ranging from 10 to 15 fm. (chem.libretexts.org)
Calculating Nucleus Diameter
The size of the nucleus can be estimated using the empirical formula:
[ R = R_0 \times A^{1/3} ]
where:
- ( R ) is the radius of the nucleus,
- ( R_0 ) is a constant approximately equal to 1.2 fm,
- ( A ) is the mass number of the nucleus (the total number of protons and neutrons).
For example, the radius of a helium-4 nucleus (with ( A = 4 )) is:
[ R = 1.2 \, \text{fm} \times 4^{1/3} \approx 1.2 \, \text{fm} \times 1.5874 \approx 1.9 \, \text{fm} ]
Thus, the diameter is approximately 3.8 fm, or 3,800 pm.
Implications
The small size of the nucleus compared to the atom as a whole explains why most of an atom’s volume is empty space. Despite its tiny size, the nucleus contains nearly all of the atom’s mass. This disparity in size and mass distribution is fundamental to understanding atomic structure and the behavior of matter at the microscopic level.
In summary, the atomic nucleus has a diameter on the order of 10 to 15 fm, which translates to 10,000 to 15,000 pm. This small size is crucial for the stability and properties of atoms, influencing chemical reactions and the formation of elements in stars.