The figure shows a conical pendulum, in which the bob (the small object at the lower end of the cord) moves in a horizontal circle at constant speed. (The cord sweeps out a cone as the bob rotates.) The bob has a mass of 0.040 kg, the string has length L = 1.1 m and negligible mass, and the bob follows a circular path of circumference 1.0 m. What are (a) the tension in the string and (b) the period of the motion?
The correct answer and explanation is :
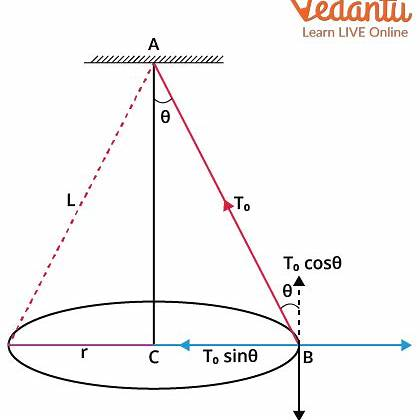
A conical pendulum consists of a mass (bob) attached to the end of a string, moving in a horizontal circular path while the string traces out a cone. In this scenario, the bob has a mass of 0.040 kg, the string length (L) is 1.1 m, and the bob follows a circular path with a circumference of 1.0 m. We aim to determine (a) the tension in the string and (b) the period of the motion.
(a) Tension in the String
First, we calculate the radius (r) of the circular path:
[ \text{Circumference} = 2\pi r ]
[ 1.0\, \text{m} = 2\pi r ]
[ r = \frac{1.0\, \text{m}}{2\pi} \approx 0.159\, \text{m} ]
The angle θ between the string and the vertical can be found using:
[ \sin\theta = \frac{r}{L} = \frac{0.159\, \text{m}}{1.1\, \text{m}} \approx 0.145 ]
[ \theta = \arcsin(0.145) \approx 8.33^\circ ]
In the vertical direction, the vertical component of the tension (T) balances the gravitational force:
[ T\cos\theta = mg ]
[ T = \frac{mg}{\cos\theta} ]
Substituting the known values:
[ T = \frac{0.040\, \text{kg} \times 9.8\, \text{m/s}^2}{\cos(8.33^\circ)} \approx 0.393\, \text{N} ]
(b) Period of the Motion
The centripetal force required for circular motion is provided by the horizontal component of the tension:
[ T\sin\theta = \frac{mv^2}{r} ]
Using the previously calculated tension and angle:
[ 0.393\, \text{N} \times \sin(8.33^\circ) = \frac{0.040\, \text{kg} \times v^2}{0.159\, \text{m}} ]
[ 0.393\, \text{N} \times 0.145 = \frac{0.040\, \text{kg} \times v^2}{0.159\, \text{m}} ]
[ 0.057\, \text{N} = \frac{0.040\, \text{kg} \times v^2}{0.159\, \text{m}} ]
Solving for v:
[ v^2 = \frac{0.057\, \text{N} \times 0.159\, \text{m}}{0.040\, \text{kg}} ]
[ v^2 \approx 0.226\, \text{m}^2/\text{s}^2 ]
[ v \approx 0.475\, \text{m/s} ]
The period (T) is the time taken for one complete revolution:
[ T = \frac{\text{Circumference}}{v} = \frac{1.0\, \text{m}}{0.475\, \text{m/s}} \approx 2.11\, \text{s} ]
Thus, the tension in the string is approximately 0.393 N, and the period of the motion is approximately 2.11 seconds.