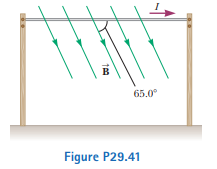
A horizontal power line of length 58.0 m carries a current of 2.20 kA northward as shown in Figure P29.41. The Earth’s magnetic field at this location has a magnitude of 5.00 10-5 T. The field at this location is directed toward the north at an angle 65.08 below the power line. Find (a) the magnitude and (b) the direction of the magnetic force on the power line.
The correct answer and explanation is :
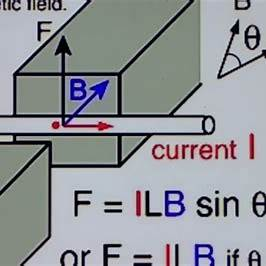
To determine the magnetic force acting on a horizontal power line carrying a current due to Earth’s magnetic field, we can use the formula for the magnetic force on a current-carrying conductor:
[ F = I \times L \times B \times \sin(\theta) ]
where:
- ( F ) is the magnetic force,
- ( I ) is the current through the wire,
- ( L ) is the length of the wire,
- ( B ) is the magnetic field strength,
- ( \theta ) is the angle between the direction of the current and the magnetic field.
Given:
- Length of the power line, ( L = 58.0 \, \text{m} ),
- Current, ( I = 2.20 \, \text{kA} = 2200 \, \text{A} ),
- Earth’s magnetic field strength, ( B = 5.00 \times 10^{-5} \, \text{T} ),
- The magnetic field is directed toward the north at an angle of 65.08° below the power line.
(a) Magnitude of the Magnetic Force
First, we need to determine the angle ( \theta ) between the current direction and the magnetic field. The current flows northward, and the magnetic field is also directed northward but at an angle of 65.08° below the horizontal. Therefore, the angle between the current direction and the magnetic field is ( \theta = 65.08^\circ ).
Now, applying the formula:
[ F = I \times L \times B \times \sin(\theta) ]
Substituting the given values:
[ F = 2200 \, \text{A} \times 58.0 \, \text{m} \times 5.00 \times 10^{-5} \, \text{T} \times \sin(65.08^\circ) ]
Calculating ( \sin(65.08^\circ) ):
[ \sin(65.08^\circ) \approx 0.9063 ]
Now, compute the force:
[ F = 2200 \times 58.0 \times 5.00 \times 10^{-5} \times 0.9063 ]
[ F \approx 5.73 \, \text{N} ]
(b) Direction of the Magnetic Force
To determine the direction of the magnetic force, we use the right-hand rule for the force on a current-carrying conductor. Point your thumb in the direction of the current (northward), and your fingers in the direction of the magnetic field (northward but downward at 65.08°). The palm then points in the direction of the force, which in this case is horizontally toward the west.
Explanation
The magnetic force on a current-carrying conductor is given by the cross product of the current element and the magnetic field:
[ \mathbf{F} = I (\mathbf{L} \times \mathbf{B}) ]
The magnitude of this force is:
[ F = I \times L \times B \times \sin(\theta) ]
where ( \theta ) is the angle between the current direction and the magnetic field. In this scenario, the current flows northward, and Earth’s magnetic field at this location is directed northward but downward at an angle of 65.08° below the horizontal. Therefore, the angle ( \theta ) between the current and the magnetic field is 65.08°.
By substituting the given values into the formula, we calculated the magnetic force to be approximately 5.73 N. The direction of this force is determined using the right-hand rule, which indicates that the force acts horizontally toward the west.
This force arises due to the interaction between the current in the power line and Earth’s magnetic field. When a current flows through a conductor in the presence of a magnetic field, it experiences a force perpendicular to both the direction of the current and the magnetic field. This phenomenon is the basis for many electromagnetic devices and is described by the Lorentz force law.