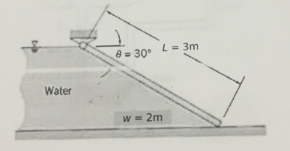
A rectangular gate of width w = 2m, and length L = 3m, and of uniform thickness so that the centre of mass is located at the centroid, holds back a depth of water at 15?C as shown.
The water surface is at the same height as the gate hinge. Find the minimum weight of the gate
so that the gate remains closed.
The correct answer and explanation is :
To determine the minimum weight required to keep the rectangular gate closed, we need to analyze the hydrostatic forces acting on the gate due to the water pressure and ensure that the gate’s weight provides sufficient counteracting moment to prevent it from opening.
Given Data:
- Width of the gate, ( w = 2 \, \text{m} )
- Length (height) of the gate, ( L = 3 \, \text{m} )
- Depth of water, ( h = 3 \, \text{m} ) (since the water surface is at the same height as the gate hinge)
- Density of water at ( 15^\circ \text{C} ), ( \rho \approx 999 \, \text{kg/m}^3 )
- Acceleration due to gravity, ( g = 9.81 \, \text{m/s}^2 )
Hydrostatic Force Calculation:
The hydrostatic force ( F_H ) acting on a submerged vertical surface is given by:
[ F_H = \rho \, g \, A \, \bar{h} ]
where:
- ( A ) is the area of the gate: ( A = w \times L = 2 \, \text{m} \times 3 \, \text{m} = 6 \, \text{m}^2 )
- ( \bar{h} ) is the depth to the centroid of the gate: ( \bar{h} = \frac{L}{2} = \frac{3 \, \text{m}}{2} = 1.5 \, \text{m} )
Substituting the values:
[ F_H = 999 \, \text{kg/m}^3 \times 9.81 \, \text{m/s}^2 \times 6 \, \text{m}^2 \times 1.5 \, \text{m} ]
[ F_H \approx 88,286.1 \, \text{N} ]
[ F_H \approx 88.3 \, \text{kN} ]
Location of Hydrostatic Force (Center of Pressure):
The center of pressure ( h_{cp} ) for a vertical surface is located below the centroid at:
[ h_{cp} = \bar{h} + \frac{I_G}{A \, \bar{h}} ]
where ( I_G ) is the second moment of area about the centroid:
[ I_G = \frac{w \, L^3}{12} = \frac{2 \, \text{m} \times (3 \, \text{m})^3}{12} = 4.5 \, \text{m}^4 ]
Therefore:
[ h_{cp} = 1.5 \, \text{m} + \frac{4.5 \, \text{m}^4}{6 \, \text{m}^2 \times 1.5 \, \text{m}} ]
[ h_{cp} = 1.5 \, \text{m} + 0.5 \, \text{m} ]
[ h_{cp} = 2 \, \text{m} ]
Moment Analysis:
To prevent the gate from opening, the moment due to the gate’s weight ( W ) about the hinge must be equal to or greater than the moment due to the hydrostatic force.
The moment arm for the hydrostatic force about the hinge is ( h_{cp} = 2 \, \text{m} ).
The weight of the gate acts through its center of mass, located at ( \bar{h} = 1.5 \, \text{m} ) from the hinge. The moment arm for the weight about the hinge is ( L – \bar{h} = 3 \, \text{m} – 1.5 \, \text{m} = 1.5 \, \text{m} ).
Setting the moments equal for equilibrium:
[ W \times 1.5 \, \text{m} = F_H \times 2 \, \text{m} ]
[ W \times 1.5 \, \text{m} = 88.3 \, \text{kN} \times 2 \, \text{m} ]
[ W = \frac{88.3 \, \text{kN} \times 2 \, \text{m}}{1.5 \, \text{m}} ]
[ W \approx 117.73 \, \text{kN} ]
Conclusion:
The minimum weight required to keep the gate closed is approximately ( 117.73 \, \text{kN} ). This weight ensures that the moment generated by the gate’s weight about the hinge counteracts the moment due to the hydrostatic force exerted by the water, thereby preventing the gate from opening.
Understanding these forces and their moments is crucial in designing gates and similar structures to ensure stability and proper functionality under fluid pressure.