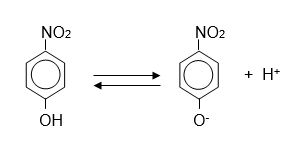
The ionization of p-nitrophenol is shown below (pKa= 7.0)
a) At pH 7, what are the relative concentrations of ionized and un-ionized p-nitrophenol?
b) If enough concentrated hydrochloric acid is added to a solution of p-nitrophenol to lower the pH from 7 to 5, what will happen to the relative concentrations of the ionized and un-ionized forms?
c) A solution of p-nitrophenol at pH 8.3 was found to have an A400 of 0.550. What is the total concentration (in um) of p-nitrophenol (ionized plus un-ionized) in the solution? The molar extinction coefficient of p-nitrophenol is 19,500M-1cm-1 and the pKa is 7.
The correct answer and explanation is :
Solution: Ionization of p-Nitrophenol
(a) Relative Concentrations at pH 7
The Henderson-Hasselbalch equation is used to determine the ratio of ionized to un-ionized p-nitrophenol:
[
\text{pH} = \text{pKa} + \log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right)
]
At pH = 7.0 and pKa = 7.0:
[
7.0 = 7.0 + \log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right)
]
[
\log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right) = 0
]
[
\frac{[\text{A}^-]}{[\text{HA}]} = 10^0 = 1
]
This means the ionized and un-ionized forms are present in equal concentrations:
[
[\text{A}^-] = [\text{HA}]
]
(b) Effect of Lowering pH to 5
If the pH is lowered from 7 to 5, the equation becomes:
[
5.0 = 7.0 + \log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right)
]
[
\log \left( \frac{[\text{A}^-]}{[\text{HA}]} \right) = -2
]
[
\frac{[\text{A}^-]}{[\text{HA}]} = 10^{-2} = 0.01
]
This means the un-ionized form ((\text{HA})) is now 100 times more abundant than the ionized form ((\text{A}^-)). Adding HCl shifts the equilibrium towards the un-ionized form.
(c) Determining Total Concentration at pH 8.3
At pH 8.3, p-nitrophenol is mostly ionized. Using Beer’s Law:
[
A = \varepsilon c l
]
where:
- ( A = 0.550 ) (absorbance at 400 nm),
- ( \varepsilon = 19,500 ) M(^{-1})cm(^{-1}) (molar extinction coefficient),
- ( l = 1.0 ) cm (path length),
- ( c ) = concentration of ionized form.
Solving for ( c ):
[
c = \frac{A}{\varepsilon l} = \frac{0.550}{(19,500)(1.0)}
]
[
c = 2.82 \times 10^{-5} M = 28.2 \, \mu M
]
Since at pH 8.3, approximately 95% of p-nitrophenol is ionized, the total concentration is:
[
\frac{28.2 \, \mu M}{0.95} \approx 29.7 \, \mu M
]
Thus, the total p-nitrophenol concentration is 29.7 μM.
Explanation
- At pH 7, the ionized and un-ionized forms are present in equal amounts.
- Lowering the pH to 5 shifts the equilibrium toward the un-ionized form, making it 100 times more prevalent than the ionized form.
- At pH 8.3, most p-nitrophenol is ionized, and its concentration is calculated using Beer’s Law. Since ionized p-nitrophenol absorbs at 400 nm, we use absorbance data to estimate its total concentration.
The ionization equilibrium of p-nitrophenol.

Here is the scientific illustration showing the ionization equilibrium of p-nitrophenol. It depicts the un-ionized (HA) and ionized (A⁻) forms, along with the effect of pH on the equilibrium shift.