Which of the following is the rotational analog of force?
(A) Angular momentum (C) moment of inertia
(B) Angular velocity (D) torque
The correct answer and explanation is :
The correct answer is (D) Torque.
Explanation:
In classical mechanics, torque is the rotational analog of force. Just as force causes a linear acceleration of an object in translational motion, torque causes a rotational acceleration of an object. Torque is a measure of the rotational force applied to an object, determining how much an object will rotate about an axis when a force is applied at a distance from that axis.
Understanding Torque:
Torque is defined mathematically as:
[
\tau = r \times F
]
where:
- ( \tau ) is the torque,
- ( r ) is the position vector from the axis of rotation to the point where the force is applied,
- ( F ) is the force vector,
- and ( \times ) represents the cross product between the vectors ( r ) and ( F ).
The magnitude of torque can also be expressed as:
[
\tau = r F \sin(\theta)
]
where:
- ( \theta ) is the angle between the position vector ( r ) and the force vector ( F ),
- ( r ) is the distance from the axis of rotation to the point where the force is applied,
- ( F ) is the applied force.
Comparison with Force:
- Force causes a linear acceleration, governed by Newton’s second law ( F = ma ), where ( m ) is mass and ( a ) is acceleration.
- Torque causes angular acceleration, governed by the rotational analog of Newton’s second law ( \tau = I \alpha ), where ( I ) is the moment of inertia and ( \alpha ) is the angular acceleration.
So, while force affects the motion of an object in a straight line, torque affects the rotation of an object around an axis.
Why Not the Other Options?
- (A) Angular momentum: Angular momentum is a property of a rotating object, similar to linear momentum, but it is not a cause of rotation.
- (B) Moment of inertia: Moment of inertia is the rotational equivalent of mass, and it is a measure of an object’s resistance to changes in its rotational motion.
- (C) Angular velocity: Angular velocity is a measure of how quickly an object rotates, but it does not cause rotation; it’s an effect of torque.
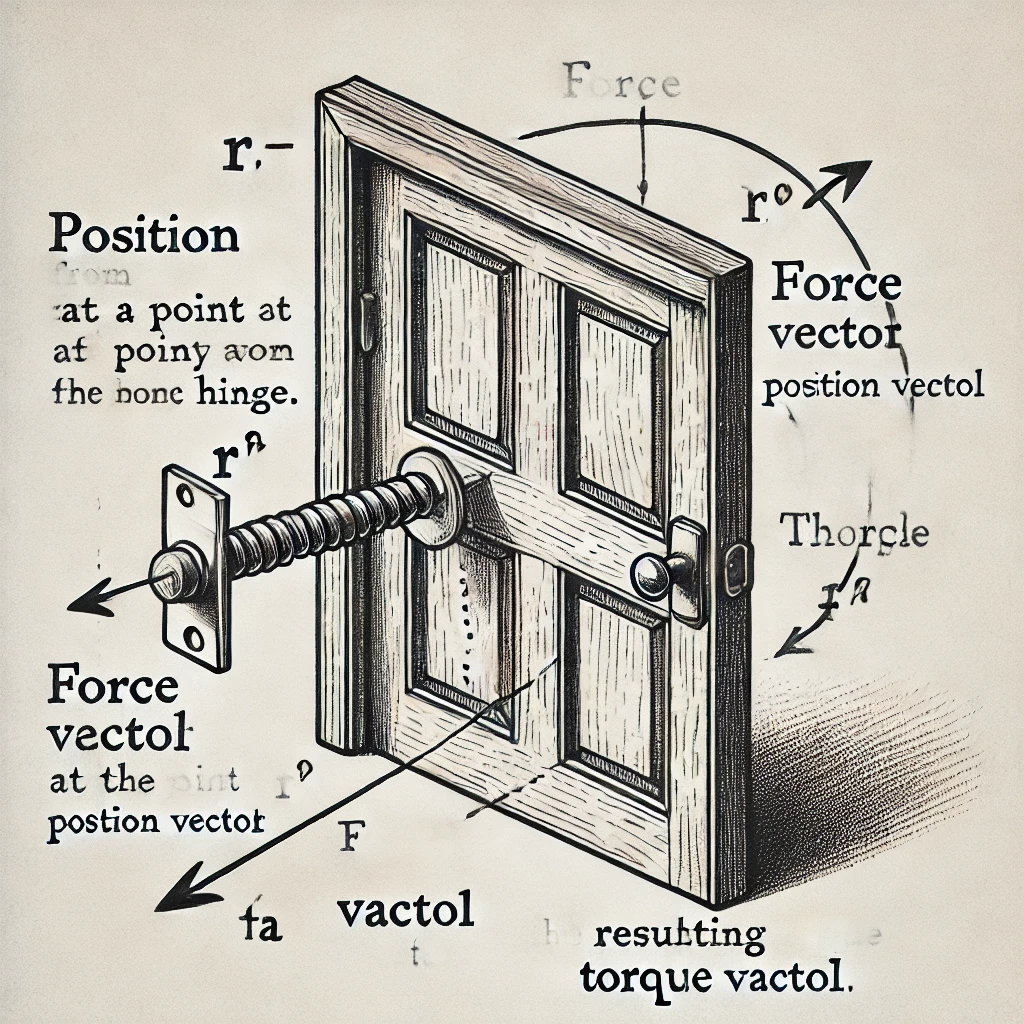
The image above illustrates the concept of torque. It shows an object (like a door) with a force applied at a point away from the hinge. The position vector (r) from the hinge to the point of force is labeled, and the force vector (F) is applied at an angle to this position vector. The angle (θ) between the force vector and position vector is also labeled, and the resulting torque vector is highlighted, showing how torque causes rotation.
This diagram should help visualize how torque works similarly to how force causes motion, but in rotational systems.