A correlation of zero between two quantitative variables means that
A. there is no linear association between the two variables
B. re-expressing the data will guarantee a linear association between the two variables
C. there is no association between the two variables
D. we have done something wrong in our calculation of r
E. none of these
The correct answer and explanation is :
The correct answer is:
A. There is no linear association between the two variables.
Explanation:
When we compute the correlation coefficient (r) between two quantitative variables, we are measuring the strength and direction of a linear relationship. The correlation coefficient r ranges from -1 to +1:
- r = +1: Perfect positive linear relationship.
- r = -1: Perfect negative linear relationship.
- r = 0: No linear relationship.
A correlation of zero (r = 0) does not mean there is no relationship at all between the variables. It only means that there is no linear relationship. The two variables may still be related in a nonlinear way.
For example, consider the relationship between x and y, where:
[
y = x^2
]
If we calculate the correlation coefficient between x and y for values symmetric around zero, we might find r = 0 because the relationship is quadratic (not linear). A scatterplot of this data would show a U-shaped curve rather than a straight line.
Why Other Answers Are Incorrect:
- B. Re-expressing the data will guarantee a linear association → Incorrect. Re-expressing (e.g., using logarithmic or square-root transformations) can sometimes reveal a linear pattern, but it is not guaranteed.
- C. There is no association between the two variables → Incorrect. A correlation of zero means no linear association, but there could still be a strong nonlinear relationship.
- D. We have done something wrong in our calculation of r → Incorrect. A correlation of zero can naturally occur in valid datasets.
Thus, the correct interpretation is that a correlation of zero means no linear association, but it does not rule out a nonlinear relationship.
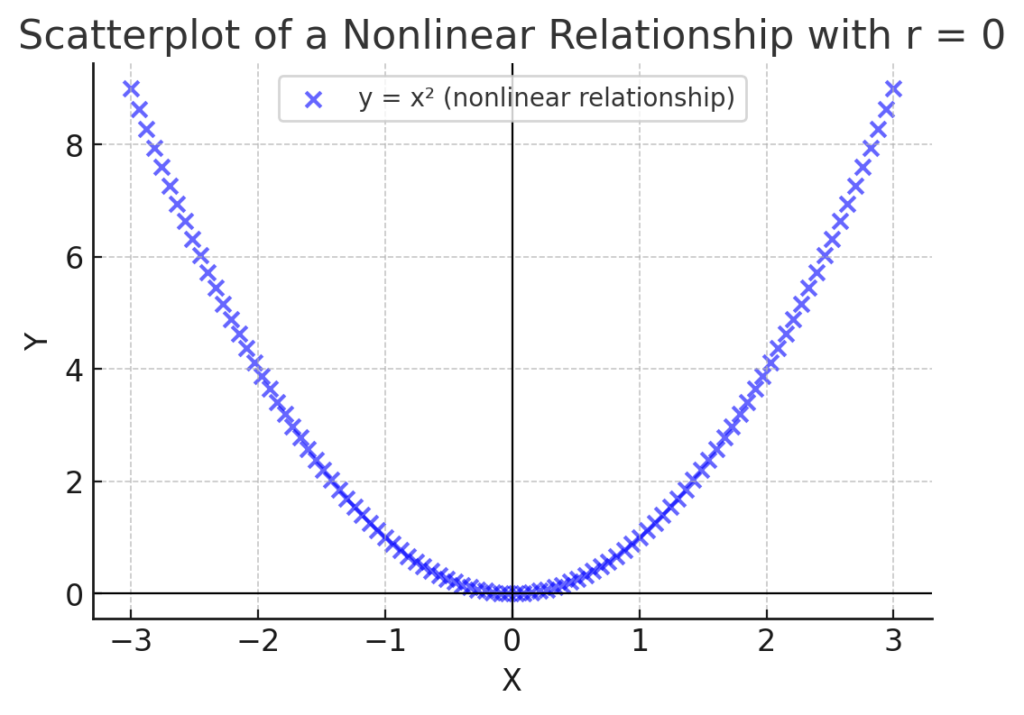
The scatterplot above shows a nonlinear relationship (a quadratic function). Even though there is a clear pattern between X and Y, the correlation coefficient r = 0 because the association is not linear. This visually demonstrates why a correlation of zero does not mean “no relationship”—it simply means no linear relationship.