From the edge of a cliff, a gun fires a pellet straight upward. The pellet’s speed after leaving the gun is 30 m/s; the cliff is 75 meters tall. Assume that the ground is at height = 0 and that the positive direction is upward. At what time does the pellet hit the ground?
The correct answer and explanation is :
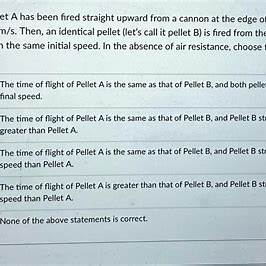
To determine the time at which a pellet, fired straight upward from the edge of a 75-meter-high cliff with an initial speed of 30 m/s, hits the ground, we can analyze the motion in two phases: the ascent and the descent.
Phase 1: Ascent
The pellet is fired upward with an initial velocity (( v_0 )) of 30 m/s. Under the influence of gravity (( g = 9.8 \, \text{m/s}^2 )), the pellet will decelerate until it reaches its peak height, where its velocity becomes zero.
Using the kinematic equation:
[ v = v_0 – g t ]
Setting the final velocity (( v )) to zero at the peak:
[ 0 = 30 \, \text{m/s} – (9.8 \, \text{m/s}^2) t_{\text{up}} ]
Solving for the time to reach the peak height (( t_{\text{up}} )):
[ t_{\text{up}} = \frac{30 \, \text{m/s}}{9.8 \, \text{m/s}^2} \approx 3.06 \, \text{s} ]
The maximum height (( h_{\text{max}} )) above the cliff can be found using:
[ h_{\text{max}} = v_0 t_{\text{up}} – \frac{1}{2} g t_{\text{up}}^2 ]
Substituting the known values:
[ h_{\text{max}} = (30 \, \text{m/s})(3.06 \, \text{s}) – \frac{1}{2} (9.8 \, \text{m/s}^2) (3.06 \, \text{s})^2 \approx 45.9 \, \text{m} ]
Therefore, the pellet reaches approximately 45.9 meters above the cliff edge, making the total height from the ground:
[ H_{\text{total}} = 75 \, \text{m} + 45.9 \, \text{m} = 120.9 \, \text{m} ]
Phase 2: Descent
From the peak, the pellet will fall back to the ground, covering a distance of 120.9 meters.
The time to fall this distance (( t_{\text{down}} )) can be calculated using the equation:
[ h = \frac{1}{2} g t_{\text{down}}^2 ]
Solving for ( t_{\text{down}} ):
[ t_{\text{down}} = \sqrt{\frac{2 h}{g}} = \sqrt{\frac{2 \times 120.9 \, \text{m}}{9.8 \, \text{m/s}^2}} \approx 4.97 \, \text{s} ]
Total Time to Hit the Ground
The total time (( t_{\text{total}} )) from firing to impact is the sum of the ascent and descent times:
[ t_{\text{total}} = t_{\text{up}} + t_{\text{down}} \approx 3.06 \, \text{s} + 4.97 \, \text{s} \approx 8.03 \, \text{s} ]
Therefore, the pellet will hit the ground approximately 8.03 seconds after being fired.
Explanation
When analyzing projectile motion, it’s essential to break the motion into distinct phases. In this scenario, the pellet’s journey can be divided into its upward ascent and downward descent. During the ascent, the pellet slows down due to gravity until it momentarily stops at its peak height. The time to reach this peak is determined by dividing the initial velocity by the acceleration due to gravity.
Once at the peak, the pellet begins its descent, accelerating downward under gravity. The total distance it falls is the sum of the cliff’s height and the additional height gained during ascent. By applying the kinematic equation for distance under constant acceleration, we can determine the time taken to fall this total distance.
Summing the times for ascent and descent provides the total duration from launch to impact. This methodical approach ensures that all aspects of the pellet’s motion are accurately accounted for, leading to a precise calculation of the total time before it hits the ground.