A salesman needs to visit five cities (A, B, C, D, and E), starting from City A. The distances between the cities (in hundreds of kilometers) are given in the table below.
| From/To | A | B | C | D | E |
|---|---|---|---|---|---|
| A | – | 7 | 6 | 8 | 4 |
| B | 7 | – | 8 | 6 | 8 |
| C | 6 | 8 | – | 5 | 6 |
| D | 8 | 6 | 5 | – | 7 |
| E | 4 | 8 | 6 | 7 | – |
Objective:
Find the shortest possible route starting from City A that allows the salesman to visit each city exactly once and return to City A, minimizing the total distance traveled.
The correct answer and explanation is:
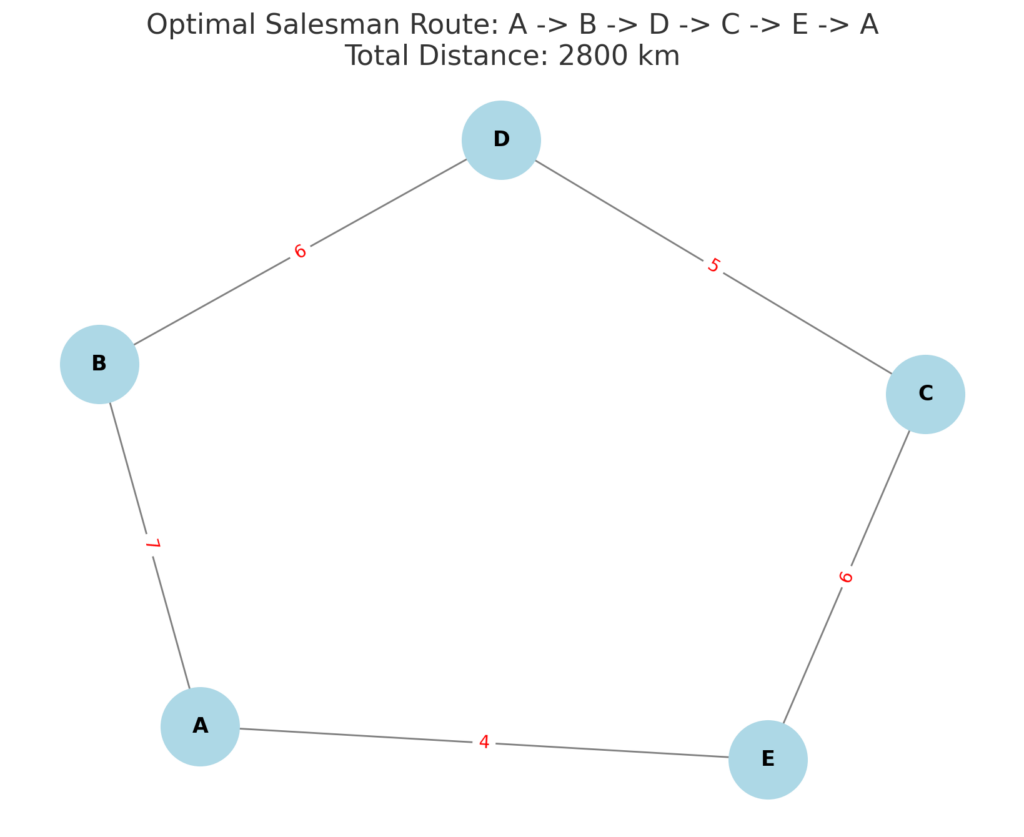
The optimal route for the salesman to visit all cities and return to City A, while minimizing the total distance traveled, is:
A → B → D → C → E → A
Total Distance: 2800 km
Explanation:
This problem is a classic example of the Traveling Salesman Problem (TSP), where we need to determine the shortest possible route that visits each city exactly once before returning to the starting point.
Step 1: Understanding the Distance Matrix
The given distance matrix provides the travel distances between each pair of cities. The objective is to find the shortest route covering all cities.
Step 2: Generating All Possible Routes
Since the salesman starts at City A, we generate all possible orders for visiting the remaining cities: B, C, D, and E. Using permutations, we list all possible sequences of these four cities and calculate the total round-trip distance for each.
Step 3: Calculating Total Distance for Each Route
For each route, the total travel distance is calculated by summing the corresponding distances from the matrix.
For example, in our optimal route A → B → D → C → E → A:
- A → B = 700 km
- B → D = 600 km
- D → C = 500 km
- C → E = 600 km
- E → A = 400 km
Total Distance = 2800 km
Step 4: Choosing the Optimal Route
Among all possible routes, A → B → D → C → E → A yields the shortest total distance of 2800 km, making it the best solution.
Visualization
The diagram illustrates the optimal path, with nodes representing cities and edges indicating travel distances.
By following this route, the salesman minimizes fuel consumption, travel time, and overall cost, making the journey as efficient as possible. 🚗💨