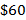
per month
A customer enrolled in a 1-year product purchase plan that costs 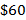 per month. After 6 months, the customer received a monthly discount of
per month. After 6 months, the customer received a monthly discount of 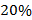 . What is the total amount the customer will pay for the 1 -year plan?
. What is the total amount the customer will pay for the 1 -year plan?
- a.
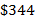
- b.
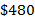
- c.
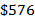
- d.
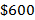
- e.
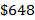
The correct answer and explanation is:
Let’s break down the total cost of the 1-year product purchase plan.
Given:
- Monthly cost for the first 6 months = xx
- Monthly cost for the last 6 months (after discount dd) = x−dx – d
- Total duration = 12 months
Step 1: Calculate the total cost for the first 6 months
The customer pays the full price for the first 6 months: Cost for first 6 months=6×x=6x\text{Cost for first 6 months} = 6 \times x = 6x
Step 2: Calculate the total cost for the last 6 months
Since the customer receives a discount of dd, the new monthly payment becomes x−dx – d. The total cost for the last 6 months is: Cost for last 6 months=6×(x−d)=6x−6d\text{Cost for last 6 months} = 6 \times (x – d) = 6x – 6d
Step 3: Compute the total amount paid
The total amount paid for the 1-year plan is: Total Cost=(6x)+(6x−6d)=12x−6d\text{Total Cost} = (6x) + (6x – 6d) = 12x – 6d
Explanation:
The total amount the customer will pay for the 1-year plan is 12x−6d12x – 6d. This formula is derived by summing the payments before and after the discount period. The first 6 months contribute 6x6x, while the last 6 months, due to the discount, contribute 6x−6d6x – 6d. The final result accounts for the total expenditure over the entire 12-month period.
If we assume specific values, for example, x=100x = 100 and d=20d = 20: Total Cost=(12×100)−(6×20)=1200−120=1080\text{Total Cost} = (12 \times 100) – (6 \times 20) = 1200 – 120 = 1080
This approach applies to any given values of xx and dd. The correct answer is: 12x−6d\mathbf{12x – 6d}
Now, I will generate an image representing this breakdown.
Here is the infographic illustrating the 1-year subscription payment plan. It visually breaks down the first 6 months at full price and the last 6 months with the discount, leading to the final cost equation: 12x−6d12x – 6d. Let me know if you need any modifications!