Mr. Thomas of Wilmer Amina Carter High School (a large urban high school) wants to know what proportion of the student body favors banning plastic water bottles from the school buildings and grounds. A simple random sample of 152 students finds that 85 support banning plastic bottles.
(a) Construct and interpret a
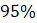
confidence interval for the proportion of all students at Wilmer Amina Carter High School who support banning plastic water bottles.
State:
Plan:
Do:
Conclude:
(b) The student council will ban the bottles if they are convinced that the majority of students favor it. Does this confidence interval provide evidence for a ban? Explain.
(c) It turns out that the council’s simple random sample was originally 165 students, but 13 individuals in the sample didn’t respond because they were on an Environmental Science field trip. Could this change your answer to part (b)? Explain your reasoning with a calculation.
(d) In part (a) you constructed a
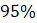
confidence interval for the proportion of students at Wilmer Amina Carter High School who support banning plastic water bottles. Explain what you would expect to happen to the length of the interval if the sample size was doubled.
The correct answer and explanation is:
Let’s break this problem down step by step.
(a) Constructing and Interpreting a Confidence Interval
State:
We want to estimate the proportion pp of all students at Wilmer Amina Carter High School who support banning plastic water bottles.
Plan:
We use a one-sample z-interval for a proportion. Conditions to check:
- Random: A simple random sample was taken.
- Normal: The sample size is large enough, confirmed by checking npnp and n(1−p)n(1-p).
- Independent: The population of students is much larger than the sample size.
Do:
The sample proportion is: p^=85152≈0.5592\hat{p} = \frac{85}{152} \approx 0.5592
Standard error: SE=p^(1−p^)n=(0.5592)(0.4408)152≈0.0403SE = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} = \sqrt{\frac{(0.5592)(0.4408)}{152}} \approx 0.0403
For a 95% confidence level, the critical z-value is 1.96.
Margin of error: ME=1.96×0.0403≈0.0790ME = 1.96 \times 0.0403 \approx 0.0790
Confidence interval: 0.5592±0.0790=(0.4802,0.6382)0.5592 \pm 0.0790 = (0.4802, 0.6382)
Conclude:
We are 95% confident that the true proportion of students who support banning plastic bottles is between 48.02% and 63.82%.
(b) Should the Bottles Be Banned?
Since the confidence interval includes 50%, we cannot be sure that a majority (more than 50%) of students favor the ban. While support might be over 50%, we lack strong enough evidence to conclude that a majority favors it.
(c) What If 13 Students Were Missing?
If the original sample was 165, but 13 did not respond, we recalculate based on 165 students.
Revised proportion: p^=85165≈0.5152\hat{p} = \frac{85}{165} \approx 0.5152
Revised standard error: SE=(0.5152)(1−0.5152)165≈0.0387SE = \sqrt{\frac{(0.5152)(1-0.5152)}{165}} \approx 0.0387
Margin of error: ME=1.96×0.0387≈0.0758ME = 1.96 \times 0.0387 \approx 0.0758
New confidence interval: 0.5152±0.0758=(0.4394,0.5910)0.5152 \pm 0.0758 = (0.4394, 0.5910)
Since the entire confidence interval is still below 50% in some cases, we still cannot be certain a majority supports the ban.
(d) What Happens If the Sample Size Doubles?
When sample size increases, the standard error decreases, making the confidence interval narrower. The confidence level remains the same, but the margin of error shrinks, leading to a more precise estimate.
If the sample size doubles, say from 152 to 304, the standard error formula shows that the interval length would decrease by a factor of 1/2≈0.7071/\sqrt{2} \approx 0.707. Thus, the interval would be about 70.7% as long, making it more precise.