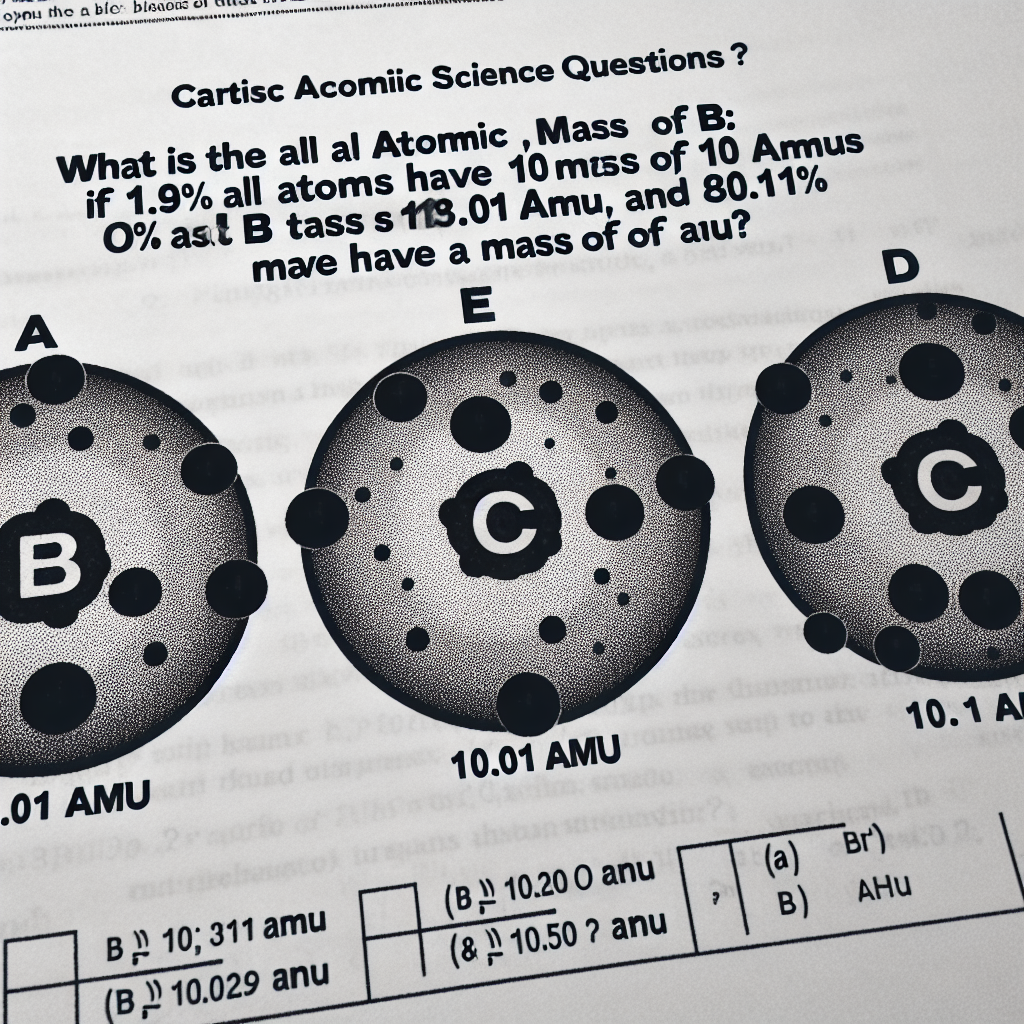
What is the atomic mass of B if 19.9% of all B atoms have a mass of 10.01 amu and 80.1% have a mass of 11.01 amu?
A) 10.21 amu
B) 10.50 amu
C) 10.63 amu
D) 10.81 amu
The correct answer and explanation is :
The atomic mass of boron (B) is calculated by considering the weighted average of its two naturally occurring isotopes: boron-10 (^10B) and boron-11 (^11B). The atomic mass of an element is not a whole number because it reflects the average mass of all its isotopes, weighted by their relative abundances.
Given Data:
- ^10B has a mass of 10.01 atomic mass units (amu) and an abundance of 19.9%.
- ^11B has a mass of 11.01 amu and an abundance of 80.1%.
Calculation:
To determine the average atomic mass of boron, we use the formula:
[ \text{Atomic Mass} = (m_1 \times f_1) + (m_2 \times f_2) ]
Where:
- ( m_1 ) and ( m_2 ) are the masses of the isotopes.
- ( f_1 ) and ( f_2 ) are the fractional abundances of the isotopes (expressed as decimals).
Applying the given values:
[ \text{Atomic Mass} = (10.01 \, \text{amu} \times 0.199) + (11.01 \, \text{amu} \times 0.801) ]
Calculating each term:
- ( 10.01 \, \text{amu} \times 0.199 = 1.990 \, \text{amu} )
- ( 11.01 \, \text{amu} \times 0.801 = 8.819 \, \text{amu} )
Summing these contributions:
[ \text{Atomic Mass} = 1.990 \, \text{amu} + 8.819 \, \text{amu} = 10.809 \, \text{amu} ]
Rounding to two decimal places, the atomic mass of boron is approximately 10.81 amu.
Answer:
The correct answer is D) 10.81 amu.
Explanation:
The atomic mass of an element is a weighted average that accounts for the masses of its isotopes and their relative abundances. In the case of boron, the more abundant isotope (^11B) has a mass of 11.01 amu, while the less abundant (^10B) has a mass of 10.01 amu. The higher abundance of ^11B pulls the average atomic mass closer to 11 amu, which is reflected in the calculated value of approximately 10.81 amu.