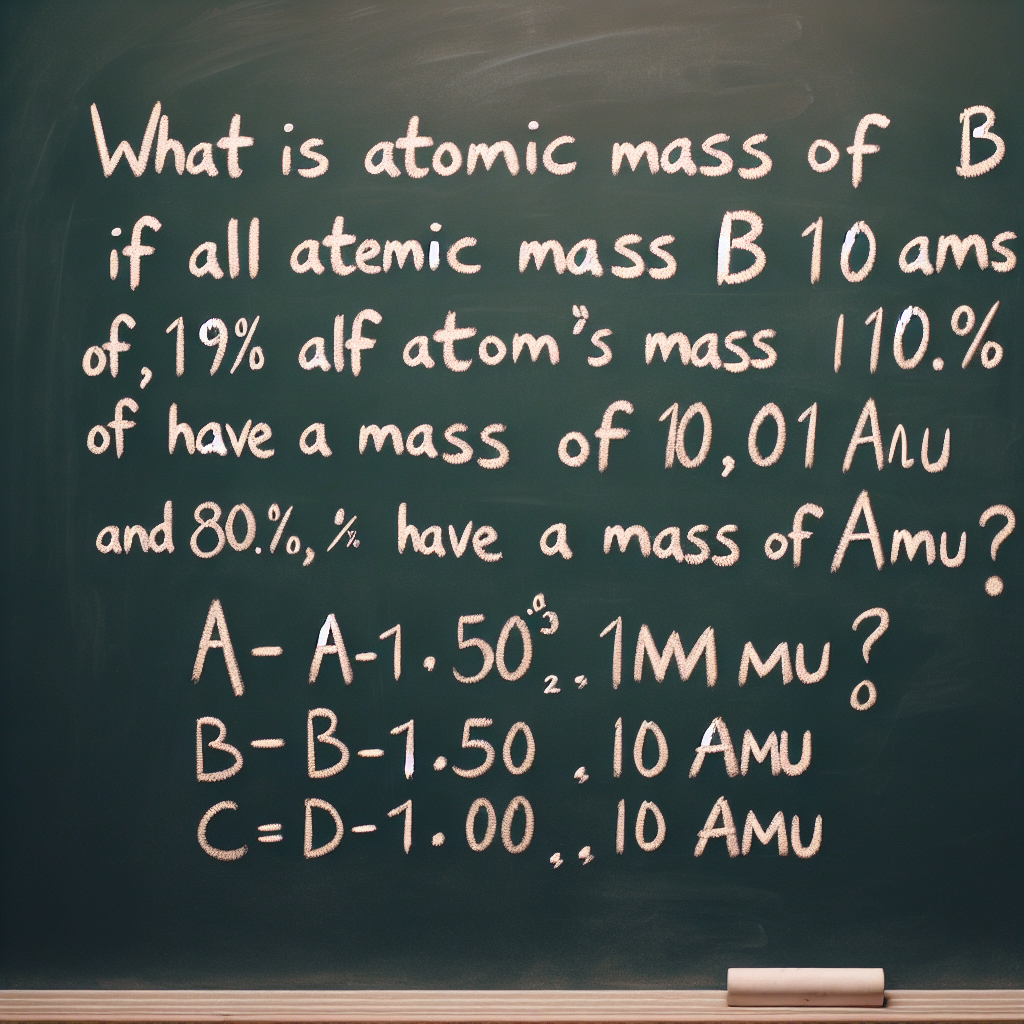What is the atomic mass of B if 19.9% of all B atoms have a mass of 10.01 amu and 80.1% have a mass of 11.01 amu?
A) 10.21 amu
B) 10.50 amu
C) 10.63 amu
D) 10.81 amu
The correct answer and explanation is :
To calculate the atomic mass of boron (( B )), we use the weighted average formula:
[
\text{Atomic Mass} = (\% \text{ abundance of isotope 1} \times \text{mass of isotope 1}) + (\% \text{ abundance of isotope 2} \times \text{mass of isotope 2})
]
Given Data:
- Isotope 1: Mass = 10.01 amu, Abundance = 19.9% (0.199 in decimal form)
- Isotope 2: Mass = 11.01 amu, Abundance = 80.1% (0.801 in decimal form)
Calculation:
[
\text{Atomic Mass} = (0.199 \times 10.01) + (0.801 \times 11.01)
]
[
= 1.990 + 8.821
]
[
= 10.811 \text{ amu}
]
Correct Answer:
D) 10.81 amu
Explanation:
The atomic mass of an element is calculated as the weighted average of its isotopes based on their natural abundance. Since boron has two stable isotopes, (^{10}B) and (^{11}B), we multiply the mass of each isotope by its respective fractional abundance and sum the results.
In this case, (^{11}B) has a much higher abundance (80.1%) compared to (^{10}B) (19.9%), which means the atomic mass of boron is closer to 11.01 amu than 10.01 amu. The computed result of 10.81 amu aligns with the periodic table value.
This approach ensures an accurate representation of boron’s atomic mass as found in nature.