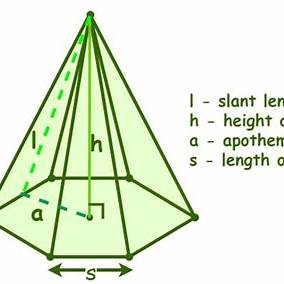
Find the volume of a regular hexagonal pyramid if the perpendicular height is 16.0cm and the side of the base is 3.0cm.
The correct answer and explanation is :
To find the volume of a regular hexagonal pyramid, we use the formula:
[
V = \frac{1}{3} \times B \times h
]
where:
- ( B ) is the area of the hexagonal base
- ( h ) is the perpendicular height of the pyramid
Step 1: Find the Area of the Hexagonal Base
A regular hexagon can be divided into six equilateral triangles. The area of one equilateral triangle with side length ( s ) is:
[
A_{\triangle} = \frac{\sqrt{3}}{4} s^2
]
Since the hexagon consists of 6 such triangles, its total area is:
[
B = 6 \times \frac{\sqrt{3}}{4} s^2
]
Substituting ( s = 3.0 ) cm:
[
B = 6 \times \frac{\sqrt{3}}{4} \times (3.0)^2
]
[
B = 6 \times \frac{\sqrt{3}}{4} \times 9
]
[
B = 6 \times \frac{9\sqrt{3}}{4}
]
[
B = \frac{54\sqrt{3}}{4}
]
[
B = \frac{27\sqrt{3}}{2} \approx 23.38 \text{ cm}^2
]
Step 2: Find the Volume
Now, using ( h = 16.0 ) cm:
[
V = \frac{1}{3} \times 23.38 \times 16.0
]
[
V = \frac{374.08}{3}
]
[
V \approx 124.69 \text{ cm}^3
]
Final Answer:
[
\mathbf{124.69 \text{ cm}^3}
]