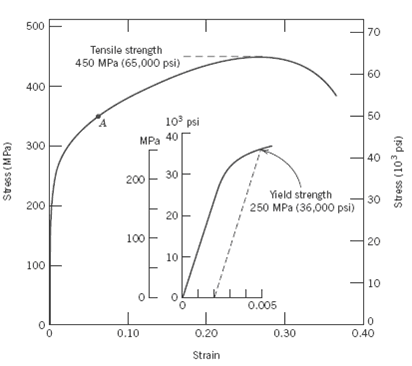
Consider the brass alloy for which the stress-strain behavior is shown in Figure 6.12. A cylindrical specimen of this material 6 mm (0.24 in.) in diameter and 50 mm (2 in.) long is pulled in tension with a force of 5000 N (1125 lbf). If it is known that this alloy has a Poisson’s ratio of 0.30, compute: (a) The specimen elongation, and (b) The reduction in specimen diameter.
The Correct Answer and Explanation is:
To solve this problem using the stress-strain curve for the brass alloy (Figure 6.12), we need to:
Given Data:
- Diameter (initial), d0d_0 = 6 mm = 0.006 m
- Length (initial), L0L_0 = 50 mm = 0.05 m
- Force, FF = 5000 N
- Poisson’s ratio, ν\nu = 0.30
Step 1: Calculate the Engineering Stress
Engineering stress, σ=FA0\sigma = \frac{F}{A_0}
Where: A0=π4d02=π4(0.006)2=2.827×10−5 m2A_0 = \frac{\pi}{4}d_0^2 = \frac{\pi}{4}(0.006)^2 = 2.827 \times 10^{-5} \text{ m}^2 σ=50002.827×10−5=176,847, Pa=176.8 MPa\sigma = \frac{5000}{2.827 \times 10^{-5}} = 176,847, \text{ Pa} = 176.8 \text{ MPa}
Step 2: Determine Strain from Stress-Strain Curve
From the graph, a stress of ~177 MPa corresponds to a strain of approximately 0.0026.
Step 3: Compute Elongation
Elongation,ΔL=ε×L0=0.0026×0.05=1.3×10−4 m=0.13 mm\text{Elongation}, \Delta L = \varepsilon \times L_0 = 0.0026 \times 0.05 = 1.3 \times 10^{-4} \text{ m} = 0.13 \text{ mm}
Step 4: Compute Reduction in Diameter
Using Poisson’s ratio: εlateral=−νεaxial=−0.30×0.0026=−0.00078\varepsilon_{\text{lateral}} = -\nu \varepsilon_{\text{axial}} = -0.30 \times 0.0026 = -0.00078 Δd=εlateral×d0=−0.00078×6=−0.00468 mm\Delta d = \varepsilon_{\text{lateral}} \times d_0 = -0.00078 \times 6 = -0.00468 \text{ mm}
Final Answers:
(a) Elongation = 0.13 mm
(b) Reduction in diameter = 0.00468 mm
Explanation
This problem involves analyzing the deformation behavior of a brass alloy under tensile loading using the provided stress-strain curve. The main goal is to determine how much a cylindrical specimen stretches and how its diameter reduces due to the applied force.
First, we calculate the engineering stress, which is the applied force divided by the original cross-sectional area of the specimen. Since the force is 5000 N and the diameter is 6 mm, the initial area is computed using the formula for the area of a circle. This gives a stress of about 176.8 MPa.
Next, we refer to the stress-strain curve to find the strain corresponding to this stress level. The curve shows that at approximately 177 MPa, the material experiences a strain of about 0.0026 (or 0.26%). Using this strain and the original length of the specimen, we calculate the elongation. It comes out to 0.13 mm.
To determine the lateral contraction (diameter reduction), we apply Poisson’s ratio. This ratio relates axial strain to lateral strain and is given as 0.30. We use it to calculate the lateral strain, which is negative since the diameter decreases when the material is stretched. Multiplying this lateral strain by the original diameter gives the reduction in diameter, approximately 0.00468 mm.
These calculations demonstrate the mechanical response of the brass alloy under elastic deformation. The elongation is small, indicating the material is within its elastic limit. The use of Poisson’s ratio allows us to understand how the material contracts laterally, maintaining volume consistency under elastic deformation.
