Lesson 6 Homework Practice Area of Composite Figures Find the area of each figure. Round to the nearest tenth if necessary. 1. 5.5 ft 3. 3 mm 14 in. 3 in. 6 in. 6 ft 9.3 mm + 14 in. -8 ft- 7.8 mm 4. 5. 12 cm 6. 1.8 m 5 yd 3.2 m 4.5 m 18 cm 19 cm 14,5 m 4.5 m 12 yd – 22 cm- 6.5 m 10 yd 2.
Lesson 6 Homework Practice
Area of compiste figures
Find the area of each figure. Round to nearest tenth if necessary
Lesson 6 Homework Practice Area of Composite Figures Find the area of each figure. Round to the nearest tenth if necessary. 1. 2. 5.5 ft 3. 4. 14 in. 3 in. 6 in. 12 yd 4 in. 10 yd 5 yd 5. 6 ft -8 ft- 18 cm 12 cm 22 cm- 19 cm 6. 9.3 mm 3.2 m 14.5 m 6.5 m 3 mm 7.8 mm 1.8 m 4.5 m 4.5 m
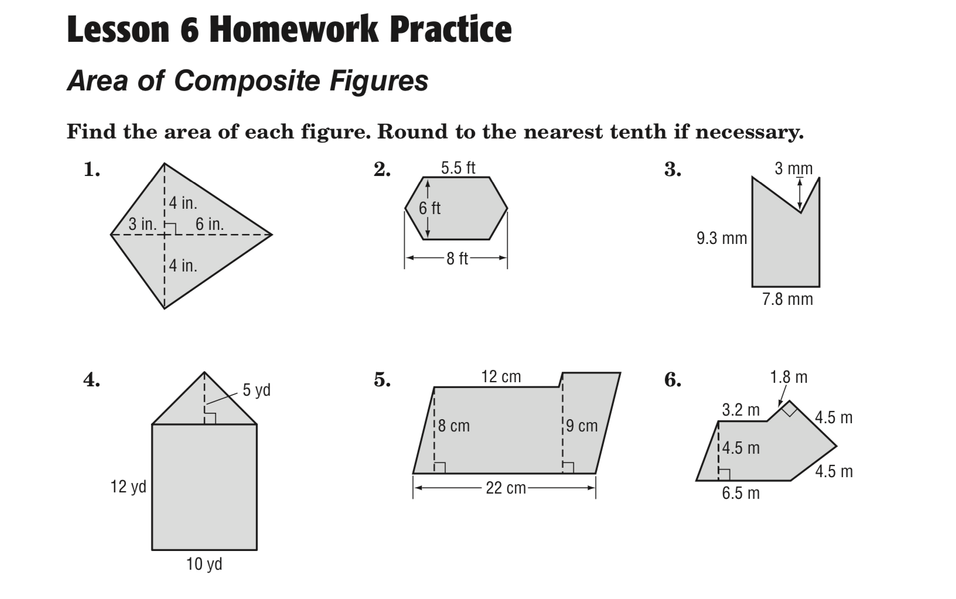
The Correct Answer and Explanation is:
:
1. Kite (Two congruent triangles)
- Top triangle: base = 6 in, height = 4 in
- Bottom triangle: base = 6 in, height = 4 in
Area of each triangle = 12×base×height=12×6×4=12\frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 6 \times 4 = 12 in²
Total area = 12+12=2412 + 12 = \boxed{24} in²
2. Trapezoid
- Bases: 6 ft and 8 ft, height = 5.5 ft
Area = 12×(base1+base2)×height\frac{1}{2} \times (\text{base}_1 + \text{base}_2) \times \text{height}
= 12×(6+8)×5.5=12×14×5.5=38.5\frac{1}{2} \times (6 + 8) \times 5.5 = \frac{1}{2} \times 14 \times 5.5 = \boxed{38.5} ft²
3. Trapezoid
- Bases: 3 mm and 7.8 mm, height = 9.3 mm
Area = 12×(3+7.8)×9.3=12×10.8×9.3=50.2\frac{1}{2} \times (3 + 7.8) \times 9.3 = \frac{1}{2} \times 10.8 \times 9.3 = \boxed{50.2} mm²
4. Composite of triangle and rectangle
- Triangle: base = 10 yd, height = 5 yd
Area = 12×10×5=25\frac{1}{2} \times 10 \times 5 = 25 yd² - Rectangle: width = 10 yd, height = 12 yd
Area = 10×12=12010 \times 12 = 120 yd²
Total area = 25+120=14525 + 120 = \boxed{145} yd²
5. Trapezoid
- Bases: 8 cm and 9 cm, height = 22 cm
Area = 12×(8+9)×22=12×17×22=187\frac{1}{2} \times (8 + 9) \times 22 = \frac{1}{2} \times 17 \times 22 = \boxed{187} cm²
6. Composite polygon
Split into:
- Triangle: base = 3.2 m, height = 1.8 m
Area = 12×3.2×1.8=2.88\frac{1}{2} \times 3.2 \times 1.8 = 2.88 m² - Trapezoid: bases = 4.5 m and 6.5 m, height = 4.5 m
Area = 12×(4.5+6.5)×4.5=12×11×4.5=24.75\frac{1}{2} \times (4.5 + 6.5) \times 4.5 = \frac{1}{2} \times 11 \times 4.5 = 24.75 m²
Total area = 2.88+24.75=27.62.88 + 24.75 = \boxed{27.6} m²
Summary of Answers:
- 24 in²
- 38.5 ft²
- 50.2 mm²
- 145 yd²
- 187 cm²
- 27.6 m²
Explanation
To find the area of composite figures, the key strategy is to break down each shape into simpler geometric components—like triangles, rectangles, or trapezoids—whose area formulas are well known. This approach allows you to apply basic formulas individually and then combine their results to find the total area.
For example, in figure 1, the shape is a kite, which is essentially two congruent triangles. Each triangle has a base and height given, and using the triangle area formula 12×base×height\frac{1}{2} \times \text{base} \times \text{height}, we calculate each and then add them for the total.
Figures like 2, 3, and 5 are trapezoids, and the trapezoid formula 12×(base1+base2)×height\frac{1}{2} \times (\text{base}_1 + \text{base}_2) \times \text{height} works efficiently here. It’s crucial to correctly identify which sides are bases (parallel) and which is the height (perpendicular distance between bases).
In figure 4, the composite figure includes a triangle on top of a rectangle. We compute the area of each separately and sum them. This approach is very common in real-world architectural and design problems where parts of objects can be rectangular with triangular additions.
Figure 6 is a more complex composite figure, combining a triangle and a trapezoid. Accurate identification of dimensions and correct application of the respective formulas help ensure the total area is found correctly.
Finally, always double-check units and round to the nearest tenth when needed. This consistent method of decomposing shapes and applying basic formulas is essential for solving any composite area problem accurately.
