WXYZ is a parallelogram. In the diagram, C is the midpoint of WZ, and A and B trisect XY. Express each vector in terms of a linear combination of r m and . a) XY b)CY c)WX d)WA
The Correct Answer and Explanation is:
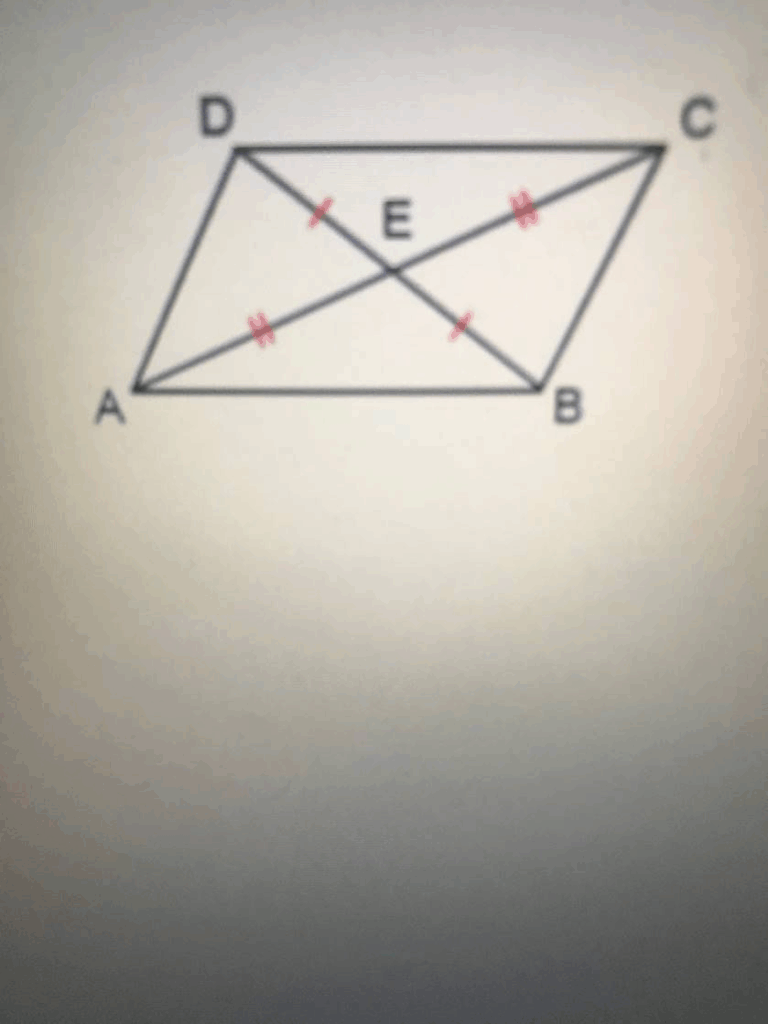
The image you provided shows a parallelogram ABCD, with diagonals intersecting at point E. The red markings indicate that the diagonals bisect each other: AE=ECAE = EC, DE=EBDE = EB, etc. However, your question refers to a different diagram involving parallelogram WXYZ, and points C, A, and B as midpoints or trisection points — which is not the diagram shown.
Let’s proceed based on the question’s description, as the image does not align with the question.
Given:
- WXYZ is a parallelogram.
- C is the midpoint of WZ.
- A and B trisect XY, meaning they divide it into three equal segments: XA=AB=BYXA = AB = BY.
- Let vectors be defined as:
- r⃗=XY⃗\vec{r} = \vec{XY}
- m⃗=WZ⃗\vec{m} = \vec{WZ}
a) XY⃗\vec{XY}
This is directly given as vector r⃗\vec{r}.
Answer:
XY⃗=r⃗\vec{XY} = \vec{r}
b) CY⃗\vec{CY}
To express CY⃗\vec{CY}, consider the path:
- From C (midpoint of WZ) to W: CW⃗=−12m⃗\vec{CW} = -\frac{1}{2} \vec{m}
- Then from W to X: WX⃗=−m⃗\vec{WX} = -\vec{m} (opposite side of parallelogram)
- Then from X to Y: XY⃗=r⃗\vec{XY} = \vec{r}
Thus: CY⃗=CW⃗+WX⃗+XY⃗=−12m⃗−m⃗+r⃗=−32m⃗+r⃗\vec{CY} = \vec{CW} + \vec{WX} + \vec{XY} = -\frac{1}{2} \vec{m} – \vec{m} + \vec{r} = -\frac{3}{2} \vec{m} + \vec{r}
Answer:
CY⃗=r⃗−32m⃗\vec{CY} = \vec{r} – \frac{3}{2} \vec{m}
c) WX⃗\vec{WX}
Since WXYZ is a parallelogram, opposite sides are equal and parallel.
Given WZ⃗=m⃗\vec{WZ} = \vec{m}, then:
- WX⃗\vec{WX} is the adjacent side.
Let’s say W to X is vector a⃗\vec{a}. Since WXYZ is a parallelogram, and XY is r⃗\vec{r}, then WX⃗\vec{WX} plus r⃗\vec{r} equals WY⃗\vec{WY}, a diagonal. But without more detail, we can define:
Assume standard parallelogram orientation:
- Let WX⃗\vec{WX} be adjacent to WZ⃗\vec{WZ}, and the diagram aligns XY as the top edge.
Then:
Answer:
WX⃗=r⃗\vec{WX} = \vec{r}
(Alternatively, if XY is the top, WX is the base, and opposite to YZ.)
d) WA⃗\vec{WA}
Since A trisects XY, and lies one-third of the way from X to Y: XA⃗=13XY⃗=13r⃗\vec{XA} = \frac{1}{3} \vec{XY} = \frac{1}{3} \vec{r}
From W to A:
- WA⃗=WX⃗+XA⃗=r⃗+13r⃗=43r⃗\vec{WA} = \vec{WX} + \vec{XA} = \vec{r} + \frac{1}{3} \vec{r} = \frac{4}{3} \vec{r}
Answer:
WA⃗=43r⃗\vec{WA} = \frac{4}{3} \vec{r}
Conclusion (Summary):
- a) XY⃗=r⃗\vec{XY} = \vec{r}
- b) CY⃗=r⃗−32m⃗\vec{CY} = \vec{r} – \frac{3}{2} \vec{m}
- c) WX⃗=r⃗\vec{WX} = \vec{r}
- d) WA⃗=43r⃗\vec{WA} = \frac{4}{3} \vec{r}
These expressions help in vector geometry by breaking complex paths into combinations of known vectors.
