We store cookies data for a seamless user experience. To know more check the Privacy Policy
Questions & Answers
Online Tutoring
Sign In
Questions » Accounting » Auditing » Attempts 0 2. Calculating marginal revenue from a…
Search Your Question Here…
Attempts 0 2. Calculating marginal revenue from a linear demand curve The blue curve on…
1 answer below »
61+
Users Viewed
23+
Downloaded Solutions
Louisiana, US
Mostly Asked From
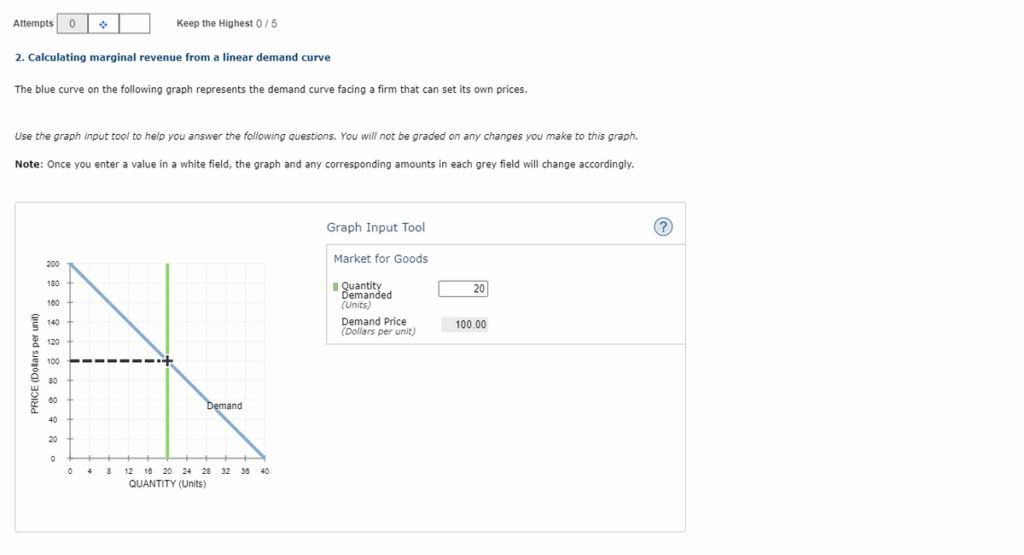
Attempts 0 2. Calculating marginal revenue from a linear demand curve The blue curve on the following graph represents the demand curve facing a firm that can set its own prices. Use the graph input tool to help you answer the following questions. You will not be graded on any changes you make to this graph. Note: Once you enter a value in a white field, the graph and any corresponding amounts in each grey field will change accordingly. PRICE (Dollars per unit) 200 180 160 140 120 100 60 40 20 0 Keep the Highest 0/5 + 0 4 8 Demand 12 16 20 24 28 32 QUANTITY (Units) 36 40 Graph Input Tool Market for Goods Quantity Demanded (Units) Demand Price (Dollars per unit) 20 100.00 ( )
The Correct Answer and Explanation is:
Correct Answer:
From the image:
- Quantity Demanded = 20 units
- Price (from Demand Curve) = $100
To calculate marginal revenue (MR) from a linear demand curve, we need to understand two key relationships:
Step-by-step Process:
1. Understand the Demand Curve:
A linear demand curve takes the form: P=a−bQP = a – bQ
Where:
- PP is price,
- QQ is quantity,
- aa is the vertical intercept (price when quantity is 0),
- bb is the slope (change in price per unit of quantity).
From the graph:
- When Q=0Q = 0, P=200P = 200
- When Q=40Q = 40, P=0P = 0
So we find the demand curve: P=200−5QP = 200 – 5Q
2. Find Total Revenue (TR):
TR=P⋅Q=(200−5Q)Q=200Q−5Q2TR = P \cdot Q = (200 – 5Q)Q = 200Q – 5Q^2
3. Differentiate to get Marginal Revenue (MR):
MR=d(TR)dQ=200−10QMR = \frac{d(TR)}{dQ} = 200 – 10Q
4. Plug in Q = 20:
MR=200−10(20)=200−200=0MR = 200 – 10(20) = 200 – 200 = 0
✅ Final Answer: Marginal Revenue at Q = 20 is $0
Explanation (300 words):
Marginal revenue (MR) refers to the additional revenue a firm earns from selling one more unit of output. When dealing with a linear demand curve, MR is not constant—it declines as output increases and is always less than the price due to the downward-sloping demand. This happens because, to sell additional units, the firm must reduce the price for all units sold, not just the last one.
In this case, the firm faces a linear demand curve: P=200−5QP = 200 – 5Q, derived from the graph. This tells us the price drops by $5 for every additional unit sold. Using this demand equation, total revenue (TR) becomes TR=P⋅Q=(200−5Q)QTR = P \cdot Q = (200 – 5Q)Q, simplifying to 200Q−5Q2200Q – 5Q^2.
Taking the derivative of total revenue with respect to quantity gives us the MR function: MR=200−10QMR = 200 – 10Q. This tells us MR decreases twice as fast as the price due to the structure of linear demand.
Plugging in Q=20Q = 20 into this MR function yields MR = 0. This point is crucial: it marks the revenue-maximizing quantity. Producing more than 20 units would cause marginal revenue to become negative, meaning the firm loses revenue on each additional unit.
Therefore, if the firm aims to maximize total revenue, it should produce exactly 20 units. Beyond this, even though it may still earn profit depending on costs, its revenue per additional unit starts to decline

.