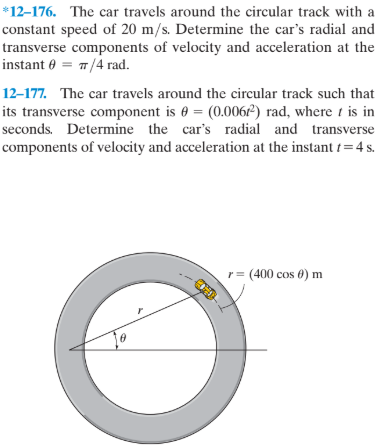
None None *12-176. The car travels around the circular track with a constant speed of 20 m/s. Determine the car’s radial and transverse components of velocity and acceleration at the instant = Ï€/4 rad. 12-177. The car travels around the circular track such that its transverse component is 0 (0.0062) rad, where t is in seconds. Determine the car’s radial and transverse components of velocity and acceleration at the instant = 4 s. O r = (400 cos 0) m
The Correct Answer and Explanation is:
Let’s solve Problem 12–177:
Given:
- Transverse angular position: θ(t) = 0.006 t² (radians)
- Time: t = 4 s
- Radius: r = 400 cos(θ) m
Step 1: Find θ, θ̇, and θ̈ at t = 4 s
θ = 0.006 t² = 0.006(4²) = 0.096 rad
Differentiate to get angular velocity and acceleration:
- θ̇ = dθ/dt = 0.012 t → θ̇(4) = 0.012(4) = 0.048 rad/s
- θ̈ = d²θ/dt² = 0.012 rad/s² (constant)
Step 2: Compute radius r and its derivatives at θ = 0.096
r = 400 cos(θ) = 400 cos(0.096) ≈ 400(0.9954) ≈ 398.17 m
Differentiate r with respect to time:
- ṙ = dr/dt = dr/dθ · dθ/dt = d(400 cosθ)/dθ · θ̇
= –400 sin(θ)·θ̇ ≈ –400 sin(0.096)(0.048) ≈ –1.837 m/s - r̈ = d²r/dt²
= d/dt(–400 sin(θ) θ̇)
= –400[cos(θ) (θ̇)² + sin(θ) θ̈]
≈ –400[cos(0.096)(0.048)² + sin(0.096)(0.012)]
≈ –400[0.9954(0.002304) + 0.0958(0.012)]
≈ –400[0.002294 + 0.00115] ≈ –400(0.003444) ≈ –1.378 m/s²
Step 3: Radial and Transverse Components
Velocity Components:
- Radial velocity: v_r = ṙ = –1.837 m/s
- Transverse velocity: v_θ = r θ̇ = 398.17 × 0.048 ≈ 19.93 m/s
Acceleration Components:
- Radial acceleration: a_r = r̈ – r(θ̇)²
= –1.378 – 398.17(0.048)² ≈ –1.378 – 0.916 ≈ –2.294 m/s² - Transverse acceleration: a_θ = r θ̈ + 2 ṙ θ̇
= 398.17(0.012) + 2(–1.837)(0.048) ≈ 4.778 – 0.176 ≈ 4.60 m/s²
Final Answers (at t = 4 s):
- Radial velocity: –1.84 m/s
- Transverse velocity: 19.93 m/s
- Radial acceleration: –2.29 m/s²
- Transverse acceleration: 4.60 m/s²
Explanation
This problem involves analyzing a car’s motion along a non-uniform circular path where both the radius and angular motion change with time. The car’s position is defined by θ(t) = 0.006t² and r = 400cos(θ). We are asked to find the radial and transverse components of velocity and acceleration at t = 4 s.
To begin, we calculate the angular position θ and its first and second derivatives, θ̇ and θ̈. These represent the angular velocity and angular acceleration. At t = 4 s, we find θ = 0.096 rad, θ̇ = 0.048 rad/s, and θ̈ = 0.012 rad/s².
The radius r at this θ is computed using the given function, resulting in r ≈ 398.17 m. Since the radius is a function of θ, which itself depends on time, we apply the chain rule to find ṙ and r̈. These values reflect how the radial distance changes over time, essential for determining radial components of motion.
Velocity in polar coordinates splits into two parts: radial (ṙ) and transverse (r θ̇). Similarly, acceleration includes a radial component (r̈ – r θ̇²) and a transverse component (r θ̈ + 2 ṙ θ̇). Substituting the calculated values yields the final answers.
The car’s transverse velocity is large (~20 m/s), while its radial velocity is negative, indicating it’s moving slightly inward at that instant. The radial acceleration is also negative, combining centripetal and radial effects, and the transverse acceleration is positive, meaning the car is speeding up angularly. These detailed components help describe the motion in curvilinear coordinates effectively.
